Deep Learning Book 6.3: Hidden Units and Activation Functions

Deep Learning
Activation Functions
Neural Networks
Author

Chao Ma

Published

September 29, 2025

This exploration of Deep Learning Chapter 6.3 reveals how activation functions shape the behavior of hidden units in neural networks - and why choosing the right one matters.

๐Ÿ““ For the complete implementation with additional exercises, see the notebook on GitHub.

๐Ÿ“š For theoretical background and summary, see the chapter summary.

Why Activation Functions Matter

Linear transformations alone can only represent linear relationships. No matter how many layers you stack, \(W_3(W_2(W_1x))\) is still just a linear function. Activation functions introduce the non-linearity that makes deep learning powerful.

But which activation function should you use? The answer depends on understanding their mathematical properties and how they affect gradient flow during training.

Activation Output Range Key Property Best For
ReLU \([0, \infty)\) Zero for negatives Hidden layers (default choice)
Sigmoid \((0, 1)\) Squashing, smooth Binary classification output
Tanh \((-1, 1)\) Zero-centered Hidden layers (when centering helps)

๐ŸŽฏ Exploring Activation Functions: Shape and Derivatives

Show code 
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn

# Set random seed for reproducibility
np.random.seed(42)
torch.manual_seed(42)

# Configure plotting
plt.rcParams['figure.facecolor'] = 'white'
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['axes.grid'] = True
plt.rcParams['grid.alpha'] = 0.3

The behavior of an activation function is determined by two things: 1. Its shape - how it transforms inputs 2. Its derivative - how gradients flow backward during training

Define Activation Functions

Show code 
def relu(x):
    return np.clip(x, 0, np.inf)

def relu_derivative(x):
    return np.where(x > 0, 1, 0)

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    return sigmoid(x) * (1 - sigmoid(x))

def tanh(x):
    return np.tanh(x)

def tanh_derivative(x):
    return 1 - np.tanh(x)**2

Plot Functions and Derivatives

Show code 
x = np.linspace(-5, 5, 1000)

fig, axes = plt.subplots(2, 3, figsize=(16, 8))
fig.suptitle('Common Activation Functions and Their Derivatives', fontsize=16)

# ReLU
axes[0, 0].plot(x, relu(x), linewidth=2, color='blue')
axes[0, 0].set_title('ReLU', fontsize=12)
axes[0, 0].set_ylabel('f(x)', fontsize=11)
axes[1, 0].plot(x, relu_derivative(x), linewidth=2, color='blue')
axes[1, 0].set_title('ReLU Derivative', fontsize=12)
axes[1, 0].set_ylabel("f'(x)", fontsize=11)
axes[1, 0].set_xlabel('x', fontsize=11)

# Sigmoid
axes[0, 1].plot(x, sigmoid(x), linewidth=2, color='red')
axes[0, 1].set_title('Sigmoid', fontsize=12)
axes[1, 1].plot(x, sigmoid_derivative(x), linewidth=2, color='red')
axes[1, 1].set_title('Sigmoid Derivative', fontsize=12)
axes[1, 1].set_xlabel('x', fontsize=11)

# Tanh
axes[0, 2].plot(x, tanh(x), linewidth=2, color='green')
axes[0, 2].set_title('Tanh', fontsize=12)
axes[1, 2].plot(x, tanh_derivative(x), linewidth=2, color='green')
axes[1, 2].set_title('Tanh Derivative', fontsize=12)
axes[1, 2].set_xlabel('x', fontsize=11)

plt.tight_layout()
plt.show()

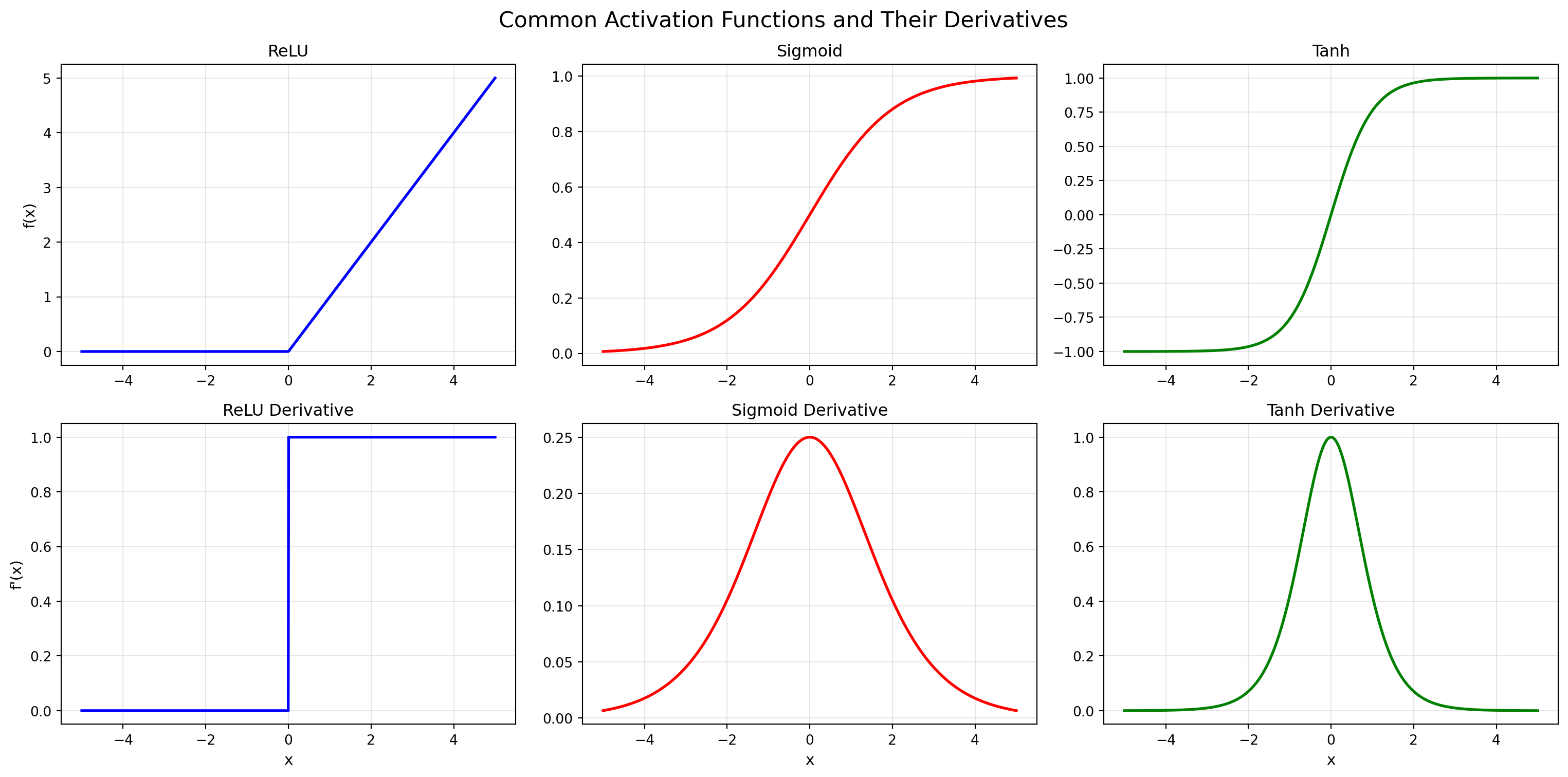
Key observations:

  • ReLU: \(f(x) = \max(0, x)\) - Zero for negative inputs, identity for positive. Derivative is 0 or 1 (simple!).
  • Sigmoid: \(f(x) = \frac{1}{1+e^{-x}}\) - Squashes inputs to \((0, 1)\). Derivative peaks at 0, vanishes at extremes (gradient vanishing problem).
  • Tanh: \(f(x) = \tanh(x)\) - Similar to sigmoid but outputs in \((-1, 1)\). Zero-centered with stronger gradients than sigmoid.

The Dead ReLU Problem: When Neurons Stop Learning

ReLUโ€™s simplicity is its strength, but also its weakness. A ReLU neuron can โ€œdieโ€ - permanently outputting zero and never learning again.

Why does this happen?

When a neuronโ€™s pre-activation values are consistently negative (due to poor initialization, high learning rate, or bad gradients), ReLU outputs zero. Since the derivative is also zero for negative inputs, no gradient flows backward. The neuron is stuck forever.

Show code 
# Generate input data
x = torch.randn(1000, 10)  # 1000 samples, 10 features
linear = nn.Linear(10, 5)   # 5 hidden units

# Set bias to large negative values to "kill" neurons
with torch.no_grad():
    linear.bias.fill_(-10.0)

# Forward pass
pre_activation = linear(x)
post_activation = torch.relu(pre_activation)

# Calculate statistics
dead_percentage = (post_activation == 0).float().mean() * 100
print(f"Percentage of dead neurons: {dead_percentage:.2f}%\n")

# Display table showing ReLU input vs output
print("ReLU Input vs Output (first 10 samples, neuron 0):")
print("-" * 50)
print(f"{'Sample':<10} {'Pre-Activation':<20} {'Post-Activation':<20}")
print("-" * 50)

for i in range(10):
    pre_val = pre_activation[i, 0].item()
    post_val = post_activation[i, 0].item()
    print(f"{i:<10} {pre_val:<20.4f} {post_val:<20.4f}")

print("\nObservation: All negative inputs become 0 after ReLU โ†’ Dead neuron!")
Percentage of dead neurons: 100.00%

ReLU Input vs Output (first 10 samples, neuron 0):
--------------------------------------------------
Sample     Pre-Activation       Post-Activation     
--------------------------------------------------
0          -9.7837              0.0000              
1          -10.0322             0.0000              
2          -10.4466             0.0000              
3          -10.3243             0.0000              
4          -10.5448             0.0000              
5          -9.7712              0.0000              
6          -10.8104             0.0000              
7          -11.3418             0.0000              
8          -9.8559              0.0000              
9          -8.6873              0.0000              

Observation: All negative inputs become 0 after ReLU โ†’ Dead neuron!

With a large negative bias, every input becomes negative after the linear transformation. ReLU zeros them all out. The gradient is zero everywhere. The neuron never updates. Itโ€™s dead.

Experiment: Do Different Activations Make a Difference?

Theory is nice, but letโ€™s see activation functions in action. Weโ€™ll train three identical networks with different activations on a simple regression task: \(y = \sin(x) + x^2 + 1\).

Generate Data

Show code 
# Training data
x_train = np.random.rand(200, 1)
y_train = np.sin(x_train) + np.power(x_train, 2) + 1

# Test data
x_test = np.random.rand(50, 1)
y_test = np.sin(x_test) + np.power(x_test, 2) + 1

# Convert to PyTorch tensors
x_train_tensor = torch.FloatTensor(x_train)
y_train_tensor = torch.FloatTensor(y_train)
x_test_tensor = torch.FloatTensor(x_test)
y_test_tensor = torch.FloatTensor(y_test)

Create and Train Models

Show code 
def create_regression_model(activation_fn):
    """Create a 2-layer network with specified activation"""
    return nn.Sequential(
        nn.Linear(1, 20),
        activation_fn,
        nn.Linear(20, 1)
    )

# Create 3 models with different activations
models = {
    'ReLU': create_regression_model(nn.ReLU()),
    'Sigmoid': create_regression_model(nn.Sigmoid()),
    'Tanh': create_regression_model(nn.Tanh())
}

# Training configuration
n_epochs = 100
learning_rate = 0.01
loss_fn = nn.MSELoss()

# Track metrics
loss_history = {name: [] for name in models.keys()}
test_mse_history = {name: [] for name in models.keys()}

# Train each model
for name, model in models.items():
    optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

    for epoch in range(n_epochs):
        # Training
        model.train()
        y_pred = model(x_train_tensor)
        loss = loss_fn(y_pred, y_train_tensor)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        loss_history[name].append(loss.item())

        # Evaluation on test set
        model.eval()
        with torch.no_grad():
            y_test_pred = model(x_test_tensor)
            test_mse = loss_fn(y_test_pred, y_test_tensor).item()
            test_mse_history[name].append(test_mse)

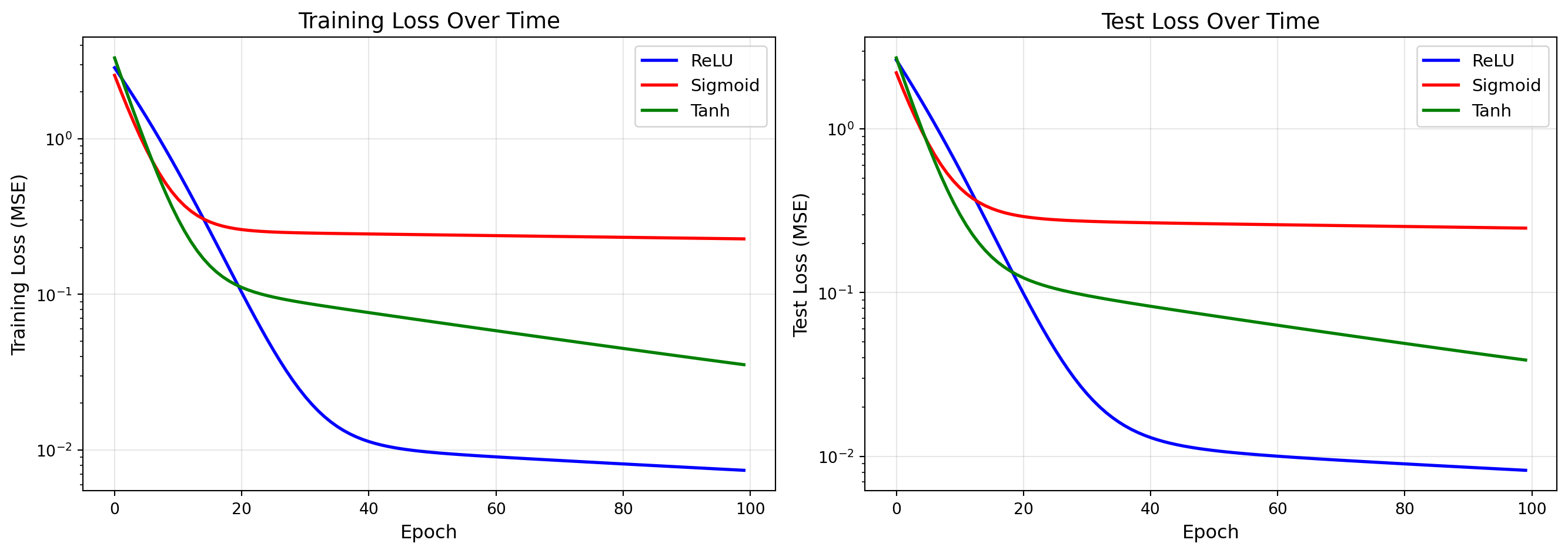
Compare Learning Curves

Show code 
fig, axes = plt.subplots(1, 2, figsize=(14, 5))
colors = {'ReLU': 'blue', 'Sigmoid': 'red', 'Tanh': 'green'}

# Plot training loss
for name, losses in loss_history.items():
    axes[0].plot(losses, label=name, linewidth=2, color=colors[name])

axes[0].set_xlabel('Epoch', fontsize=12)
axes[0].set_ylabel('Training Loss (MSE)', fontsize=12)
axes[0].set_title('Training Loss Over Time', fontsize=14)
axes[0].legend(fontsize=11)
axes[0].grid(True, alpha=0.3)
axes[0].set_yscale('log')

# Plot test MSE
for name, test_mse in test_mse_history.items():
    axes[1].plot(test_mse, label=name, linewidth=2, color=colors[name])

axes[1].set_xlabel('Epoch', fontsize=12)
axes[1].set_ylabel('Test Loss (MSE)', fontsize=12)
axes[1].set_title('Test Loss Over Time', fontsize=14)
axes[1].legend(fontsize=11)
axes[1].grid(True, alpha=0.3)
axes[1].set_yscale('log')

plt.tight_layout()
plt.show()

# Print final metrics
print("\nFinal Metrics after {} epochs:".format(n_epochs))
print("-" * 60)
print(f"{'Activation':<15} {'Train Loss':<15} {'Test Loss':<15}")
print("-" * 60)
for name in models.keys():
    train_loss = loss_history[name][-1]
    test_loss = test_mse_history[name][-1]
    print(f"{name:<15} {train_loss:<15.6f} {test_loss:<15.6f}")


Final Metrics after 100 epochs:
------------------------------------------------------------
Activation      Train Loss      Test Loss      
------------------------------------------------------------
ReLU            0.007420        0.008211       
Sigmoid         0.227441        0.247947       
Tanh            0.035384        0.038743