MIT 18.06SC Lecture 9: Independence, Basis, and Dimension
Context
This lecture develops three fundamental concepts: linear independence (no redundancy), basis (minimal spanning set), and dimension (fundamental measure of vector space size). These concepts unify our understanding of vector spaces through the rank-nullity theorem.
Linear Independence
Definition
Vectors \(x_1, x_2, \ldots, x_n\) are linearly independent if the only linear combination that produces the zero vector is the trivial combination (all coefficients zero):
\[ c_1x_1 + c_2x_2 + \cdots + c_nx_n = 0 \quad \Rightarrow \quad c_1 = c_2 = \cdots = c_n = 0 \]
Equivalently, vectors are dependent if there exists a non-trivial combination (some \(c_i \neq 0\)) that gives zero:
\[ c_1x_1 + c_2x_2 + \cdots + c_nx_n = 0 \quad \text{with some } c_i \neq 0 \]
When Are Vectors Dependent?
Case 1: Zero vector present
If one of the vectors is \(\vec{0}\), the vectors are automatically dependent: \[ r \cdot \vec{0} + 0 \cdot x_1 + \cdots + 0 \cdot x_n = 0 \quad \text{(non-trivial combination)} \]
Case 2: Vectors in the same direction (collinear)
If any two vectors are scalar multiples of each other, the set is dependent.
Example: Vectors \(v_1 = \begin{bmatrix} 1 \\ 2 \end{bmatrix}\) and \(v_2 = \begin{bmatrix} 2 \\ 4 \end{bmatrix}\) are dependent because: \[ 2v_1 - v_2 = 2\begin{bmatrix} 1 \\ 2 \end{bmatrix} - \begin{bmatrix} 2 \\ 4 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \]
General case: If \(v_2 = cv_1\) for some scalar \(c\), then: \[ cv_1 - v_2 = 0 \quad \text{(non-trivial combination)} \]
Case 3: More vectors than dimensions (\(n > m\))
If we have \(n\) vectors in \(\mathbb{R}^m\) with \(n > m\), and the first \(m\) vectors are linearly independent (not collinear/coplanar), then all \(n\) vectors must be dependent.
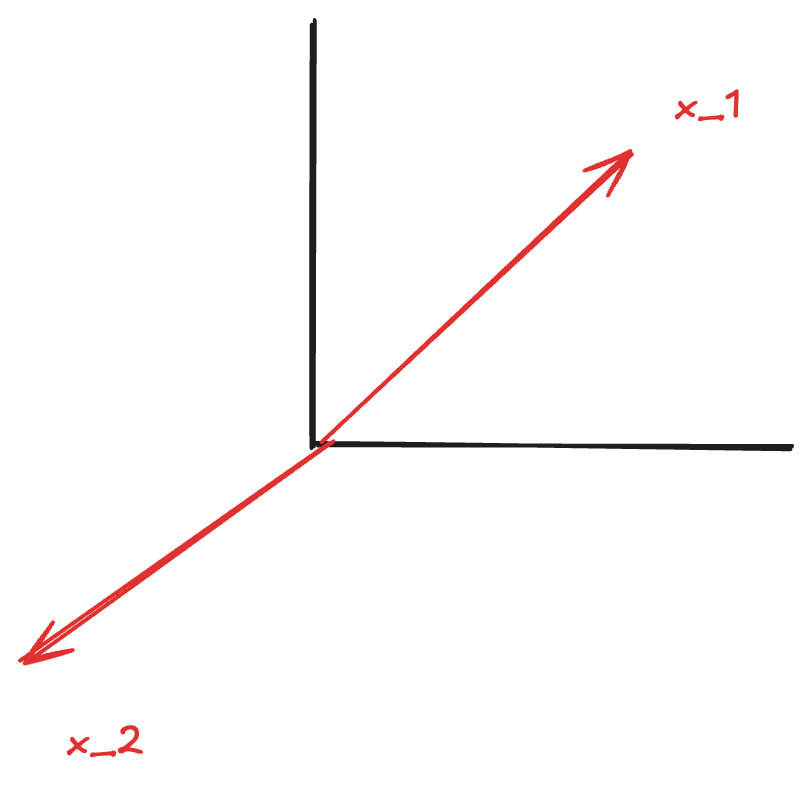
Example in \(\mathbb{R}^2\): Consider three vectors \(x_1, x_2, x_3\) in the plane where \(x_1\) and \(x_2\) are not collinear.
- Since \(x_1\) and \(x_2\) are linearly independent, their combinations \(c_1x_1 + c_2x_2\) span the entire plane
- Therefore, \(x_3\) can be expressed as some combination of \(x_1\) and \(x_2\)
- This means we can find \(c_1, c_2\) such that \(c_1x_1 + c_2x_2 = x_3\)
- Rearranging: \(c_1x_1 + c_2x_2 - x_3 = 0\) (a non-trivial combination equals zero)
- Thus \(x_1, x_2, x_3\) are dependent
Null Space Interpretation
To test independence of vectors \(v_1, v_2, \ldots, v_n\), form the matrix: \[ A = [v_1 \mid v_2 \mid \cdots \mid v_n] \]
The equation \(c_1v_1 + c_2v_2 + \cdots + c_nv_n = 0\) becomes \(Ax = 0\) where \(x = \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_n \end{bmatrix}\).
Vectors are independent if and only if: - \(N(A) = \{\vec{0}\}\) (null space contains only zero vector) - \(\text{rank}(A) = n\) (full column rank) - No free variables
Vectors are dependent if and only if: - \(N(A)\) contains non-zero vectors - \(\text{rank}(A) < n\) (rank deficient) - Has free variables (\(n - r > 0\))
Example: For 3 vectors in \(\mathbb{R}^2\) (underdetermined system with \(m = 2 < n = 3\)): - We have \(r = 2 = m < n = 3\) - Number of free variables: \(n - r = 3 - 2 = 1\) - \(N(A)\) has infinitely many solutions - Therefore, the vectors are dependent
Spanning Sets
Definition
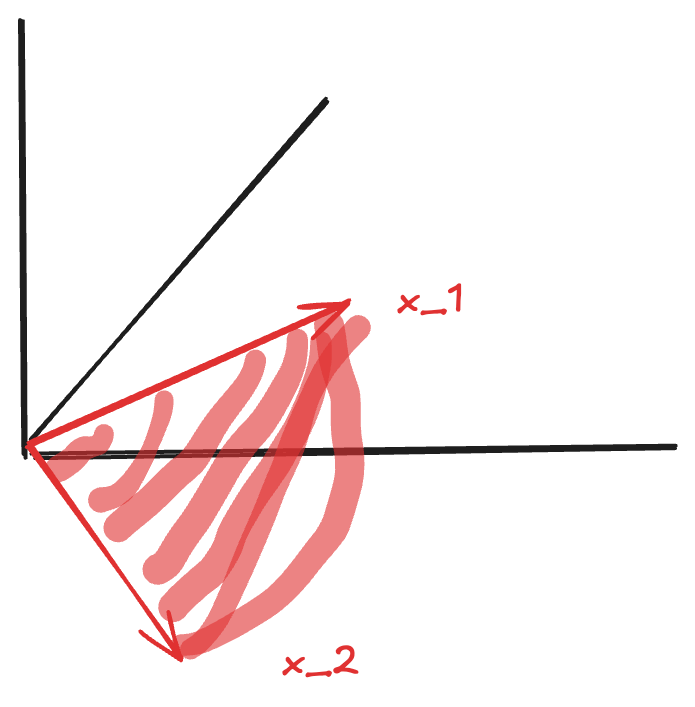
Vectors \(v_1, v_2, \ldots, v_l\) span a space \(S\) if every vector in \(S\) can be written as a linear combination of \(v_1, \ldots, v_l\):
\[ S = \text{span}(v_1, \ldots, v_l) = \{c_1v_1 + c_2v_2 + \cdots + c_lv_l \mid c_i \in \mathbb{R}\} \]
Interpretation: The span is the set of all possible linear combinations of the vectors.
Basis
Definition
A basis for a vector space \(S\) is a sequence of vectors \(v_1, v_2, \ldots, v_n\) that satisfies two properties:
- Independence: The vectors are linearly independent
- Ensures no redundancy (can’t remove any vector)
- Rank = number of vectors
- Spanning: The vectors span the space \(S\)
- Every vector in \(S\) can be expressed as a combination
- Rank = dimension of space
Key insight: A basis is a minimal spanning set (independent) and a maximal independent set (spanning).
Standard Basis for \(\mathbb{R}^n\)
For the space \(\mathbb{R}^n\), the standard basis consists of \(n\) vectors.
Example in \(\mathbb{R}^3\): \[ \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \quad \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \quad \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \]
These are the columns of the identity matrix \(I_3\).
Properties of Bases
Every vector has a unique representation: If \(\{v_1, \ldots, v_n\}\) is a basis for \(S\), then every \(x \in S\) can be written uniquely as: \[ x = c_1v_1 + c_2v_2 + \cdots + c_nv_n \]
All bases have the same size: Any two bases for the same space have the same number of vectors (this number is the dimension)
Basis matrix is invertible: If we form a matrix \(B = [v_1 \mid \cdots \mid v_n]\) where \(\{v_1, \ldots, v_n\}\) is a basis for \(\mathbb{R}^n\), then \(B\) is square (\(n \times n\)) and invertible
Dimension
Definition
The dimension of a vector space \(S\) is the number of vectors in any basis for \(S\).
Notation: \(\dim(S)\)
Dimension Formulas
For an \(m \times n\) matrix \(A\) with rank \(r\):
Dimension of column space: \[ \dim(C(A)) = r \] The pivot columns form a basis for \(C(A)\).
Dimension of null space (also called nullity): \[ \dim(N(A)) = n - r \] The number of special solutions equals the number of free variables.
Rank-Nullity Theorem: \[ \dim(C(A)) + \dim(N(A)) = n \] or equivalently: \[ r + (n - r) = n \]
Examples
Example 1: Matrix with full column rank \[ A = \begin{bmatrix} 1 & 0 \\ 2 & 1 \\ 3 & 2 \end{bmatrix}, \quad r = 2, \, m = 3, \, n = 2 \]
- \(\dim(C(A)) = 2\) (columns are independent, they form a basis)
- \(\dim(N(A)) = n - r = 2 - 2 = 0\) (only zero vector in null space)
Example 2: Rank-deficient matrix \[ A = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \end{bmatrix}, \quad r = 1, \, m = 2, \, n = 3 \]
- \(\dim(C(A)) = 1\) (only one independent column)
- \(\dim(N(A)) = n - r = 3 - 1 = 2\) (2-dimensional null space)
Summary
| Concept | Definition | Test |
|---|---|---|
| Independence | No non-trivial combination gives zero | \(N(A) = \{\vec{0}\}\) or \(r = n\) |
| Spanning | All vectors in space are combinations | \(C(A) = S\) or \(r = \dim(S)\) |
| Basis | Independent + Spanning | \(r = n = \dim(S)\) |
| Dimension | Number of vectors in basis | \(\dim(C(A)) = r\), \(\dim(N(A)) = n - r\) |
Key relationships: - Independence prevents redundancy (no vector is a combination of others) - Spanning ensures completeness (every vector in the space is reachable) - Basis achieves both: minimal spanning set = maximal independent set - Dimension is the fundamental measure of “size” of a vector space
Source: MIT 18.06SC Linear Algebra, Lecture 9