Lecture 29: Singular Value Decomposition
Overview
This lecture introduces the Singular Value Decomposition (SVD), one of the most important matrix factorizations:
- Geometric interpretation: how \(A\) maps the row space to the column space
- The fundamental SVD equation: \(A = U\Sigma V^{\top}\)
- Computing SVD through \(A^{\top}A\) and \(AA^{\top}\)
- Full rank example with complete computation
- Singular (rank-deficient) example
- Geometric meaning: orthonormal bases for all four fundamental subspaces
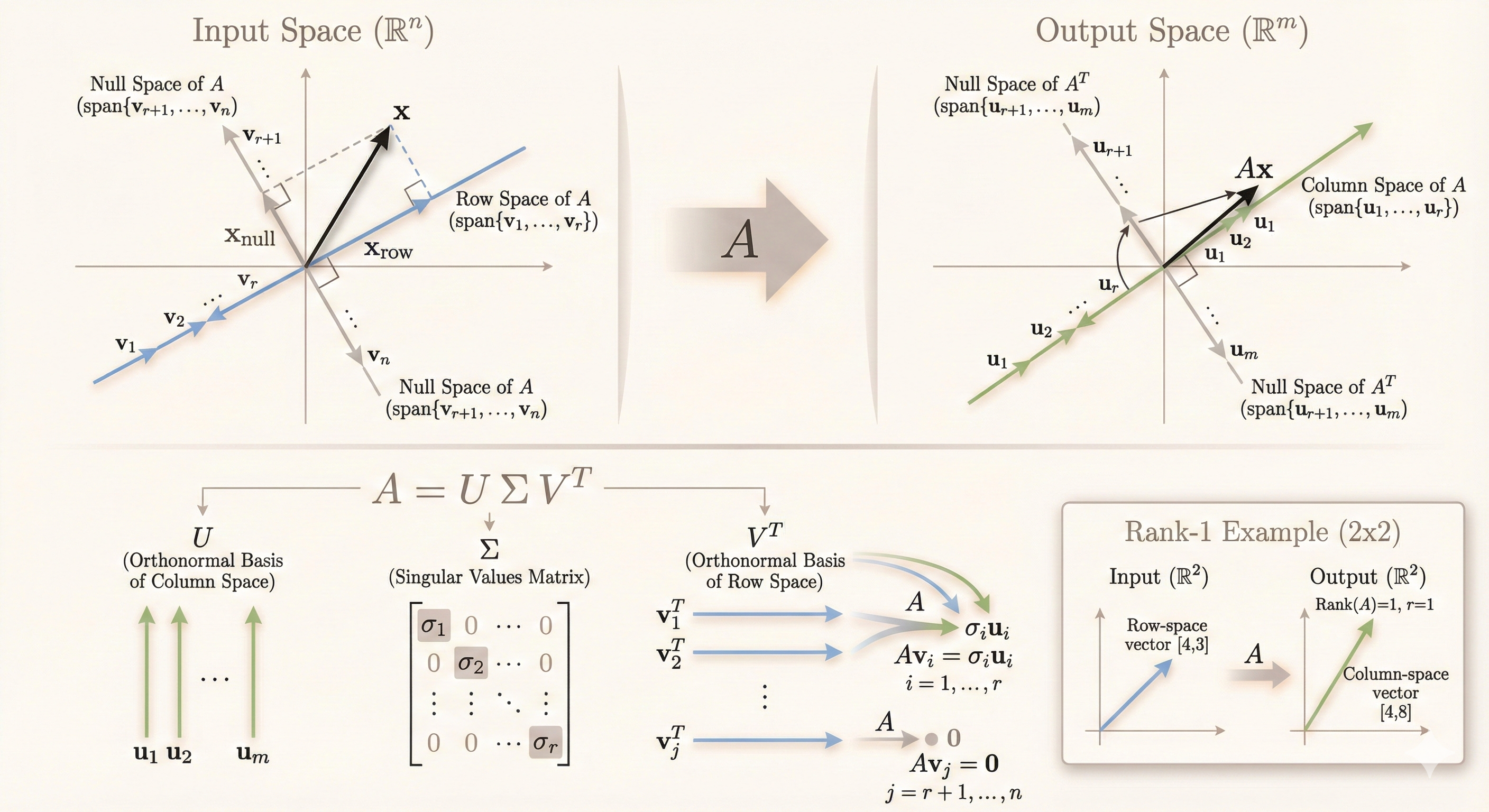 Figure: The Singular Value Decomposition provides orthonormal bases for all four fundamental subspaces, revealing how a matrix transforms space.
Figure: The Singular Value Decomposition provides orthonormal bases for all four fundamental subspaces, revealing how a matrix transforms space.
1. Understanding \(Ax\): What Does a Matrix See and Do?
What Can \(A\) See? (Input Side)
When computing \(Ax\), the matrix \(A\) only “sees” the component of \(x\) that lies in the row space of \(A\).
Key insight: Any component of \(x\) in the nullspace of \(A\) is invisible to \(A\) and gets mapped to zero.
Mathematically: - Decompose \(x = x_{\text{row}} + x_{\text{null}}\) where: - \(x_{\text{row}} \in \text{Row}(A)\) - \(x_{\text{null}} \in \text{Null}(A)\) - Then \(Ax = A(x_{\text{row}} + x_{\text{null}}) = Ax_{\text{row}} + 0 = Ax_{\text{row}}\)
Where Does \(Ax\) Go? (Output Side)
The result \(Ax\) always lies in the column space of \(A\), because \(Ax\) is a linear combination of the columns of \(A\):
\[ Ax = x_1 c_1 + x_2 c_2 + \cdots + x_n c_n \]
where \(c_i\) are the columns of \(A\).
The Complete Picture
The full action of \(A\): 1. Extract the projection of \(x\) onto the row space 2. Map that projection into the column space
This is precisely what SVD makes explicit!
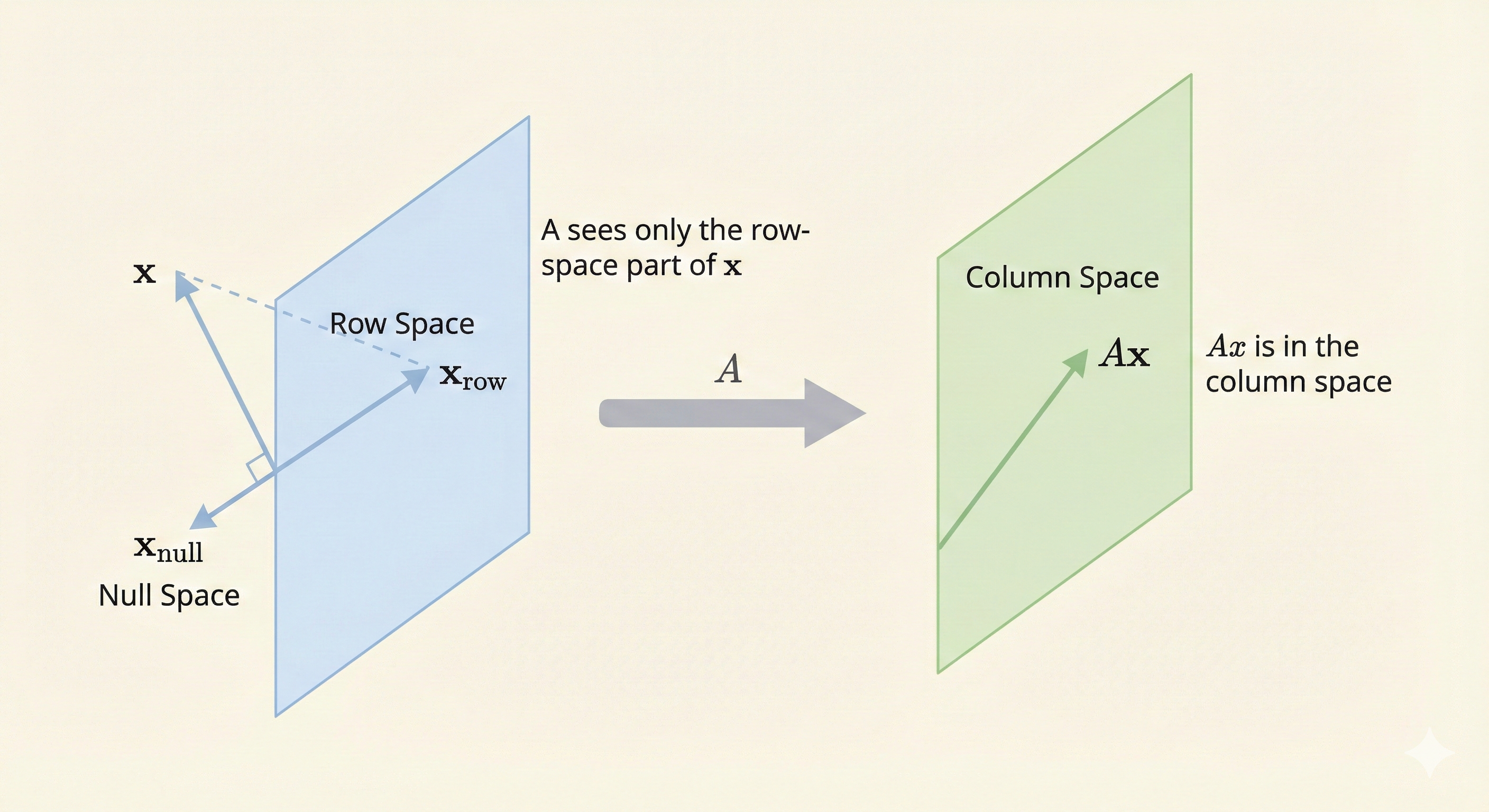 Figure: Matrix \(A\) maps vectors from its row space to its column space. Components in the nullspace vanish.
Figure: Matrix \(A\) maps vectors from its row space to its column space. Components in the nullspace vanish.
2. The SVD Equation: \(AV = U\Sigma\)
Fundamental Relationship
The singular value decomposition expresses how \(A\) maps orthonormal vectors in its row space to scaled orthonormal vectors in its column space:
\[ \sigma_i u_i = A v_i \]
for \(i = 1, 2, \ldots, r\) where \(r = \text{rank}(A)\).
Matrix Form
\[ A \begin{bmatrix} v_1 & v_2 & \cdots & v_r \end{bmatrix} = \begin{bmatrix} u_1 & u_2 & \cdots & u_r \end{bmatrix} \begin{bmatrix} \sigma_1 & & \\ & \sigma_2 & \\ & & \ddots \end{bmatrix} \]
Key properties: - \(r\): rank of \(A\) - \(V = [v_1, v_2, \ldots, v_r]\): orthonormal basis for row space - \(U = [u_1, u_2, \ldots, u_r]\): orthonormal basis for column space - \(\Sigma\): diagonal matrix of singular values \(\sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r > 0\)
Full SVD Form
For an \(m \times n\) matrix \(A\) of rank \(r\):
\[ A = U \Sigma V^{\top} \]
where: - \(U\): \(m \times m\) orthogonal matrix (left singular vectors) - \(\Sigma\): \(m \times n\) diagonal matrix (singular values) - \(V\): \(n \times n\) orthogonal matrix (right singular vectors)
Since \(V\) is orthogonal: \(V^{-1} = V^{\top}\).
3. Computing SVD via \(A^{\top}A\) and \(AA^{\top}\)
Strategy
The key insight is that: - \(A^{\top}A\) gives us \(V\) and \(\sigma^2\) values - \(AA^{\top}\) gives us \(U\) and \(\sigma^2\) values
Derivation for \(A^{\top}A\)
\[ A^{\top}A = (U\Sigma V^{\top})^{\top} (U\Sigma V^{\top}) = V\Sigma^{\top} U^{\top} U \Sigma V^{\top} \]
Since \(U^{\top}U = I\) (orthonormal):
\[ A^{\top}A = V \Sigma^{\top} \Sigma V^{\top} = V \begin{bmatrix} \sigma_1^2 & & \\ & \sigma_2^2 & \\ & & \ddots \end{bmatrix} V^{\top} \]
Conclusion: \(A^{\top}A\) is symmetric with: - Eigenvectors: columns of \(V\) (right singular vectors) - Eigenvalues: \(\sigma_i^2\) (squared singular values)
Derivation for \(AA^{\top}\)
Similarly:
\[ AA^{\top} = U\Sigma V^{\top} V \Sigma^{\top} U^{\top} = U \Sigma \Sigma^{\top} U^{\top} = U \begin{bmatrix} \sigma_1^2 & & \\ & \sigma_2^2 & \\ & & \ddots \end{bmatrix} U^{\top} \]
Conclusion: \(AA^{\top}\) is symmetric with: - Eigenvectors: columns of \(U\) (left singular vectors) - Eigenvalues: \(\sigma_i^2\) (same squared singular values)
4. Example 1: Full Rank Matrix
Problem
\[ A = \begin{bmatrix} 4 & 4 \\ -3 & 3 \end{bmatrix} \]
Goal: Find \(V, \Sigma, U\) such that \(A = U\Sigma V^{\top}\).
Step 1: Compute \(A^{\top}A\)
\[ A^{\top}A = \begin{bmatrix} 4 & -3 \\ 4 & 3 \end{bmatrix} \begin{bmatrix} 4 & 4 \\ -3 & 3 \end{bmatrix} = \begin{bmatrix} 25 & 7 \\ 7 & 25 \end{bmatrix} \]
Step 2: Find Eigenvalues and Eigenvectors of \(A^{\top}A\)
Eigenvalue 1: \(\lambda_1 = 32\)
\[ \begin{bmatrix} 25 & 7 \\ 7 & 25 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = 32 \begin{bmatrix} 1 \\ 1 \end{bmatrix} \]
Eigenvalue 2: \(\lambda_2 = 18\)
\[ \begin{bmatrix} 25 & 7 \\ 7 & 25 \end{bmatrix} \begin{bmatrix} 1 \\ -1 \end{bmatrix} = 18 \begin{bmatrix} 1 \\ -1 \end{bmatrix} \]
Step 3: Form \(\Sigma\) and \(V\)
Singular values:
\[ \sigma_1 = \sqrt{32} = 4\sqrt{2}, \quad \sigma_2 = \sqrt{18} = 3\sqrt{2} \]
\[ \Sigma = \begin{bmatrix} \sqrt{32} & 0 \\ 0 & \sqrt{18} \end{bmatrix} = \begin{bmatrix} 4\sqrt{2} & 0 \\ 0 & 3\sqrt{2} \end{bmatrix} \]
Right singular vectors (normalize eigenvectors):
\[ V = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} \]
Step 4: Compute \(AA^{\top}\)
\[ AA^{\top} = \begin{bmatrix} 4 & 4 \\ -3 & 3 \end{bmatrix} \begin{bmatrix} 4 & -3 \\ 4 & 3 \end{bmatrix} = \begin{bmatrix} 32 & 0 \\ 0 & 18 \end{bmatrix} \]
Note: \(AA^{\top}\) is already diagonal!
Step 5: Find Eigenvectors of \(AA^{\top}\)
Eigenvalue 1: \(\lambda_1 = 32\)
\[ \begin{bmatrix} 32 & 0 \\ 0 & 18 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = 32 \begin{bmatrix} 1 \\ 0 \end{bmatrix} \]
Eigenvalue 2: \(\lambda_2 = 18\)
\[ \begin{bmatrix} 32 & 0 \\ 0 & 18 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = 18 \begin{bmatrix} 0 \\ 1 \end{bmatrix} \]
Wait, there’s a sign issue! Let me check with \(Av_i = \sigma_i u_i\):
For consistency, we should have:
\[ u_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \quad u_2 = \begin{bmatrix} 0 \\ -1 \end{bmatrix} \]
(The sign of \(u_2\) must match \(Av_2 = \sigma_2 u_2\).)
Left singular vectors:
\[ U = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \]
Final SVD
\[ A = U\Sigma V^{\top} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \begin{bmatrix} 4\sqrt{2} & 0 \\ 0 & 3\sqrt{2} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} \]
5. Example 2: Singular (Rank 1) Matrix
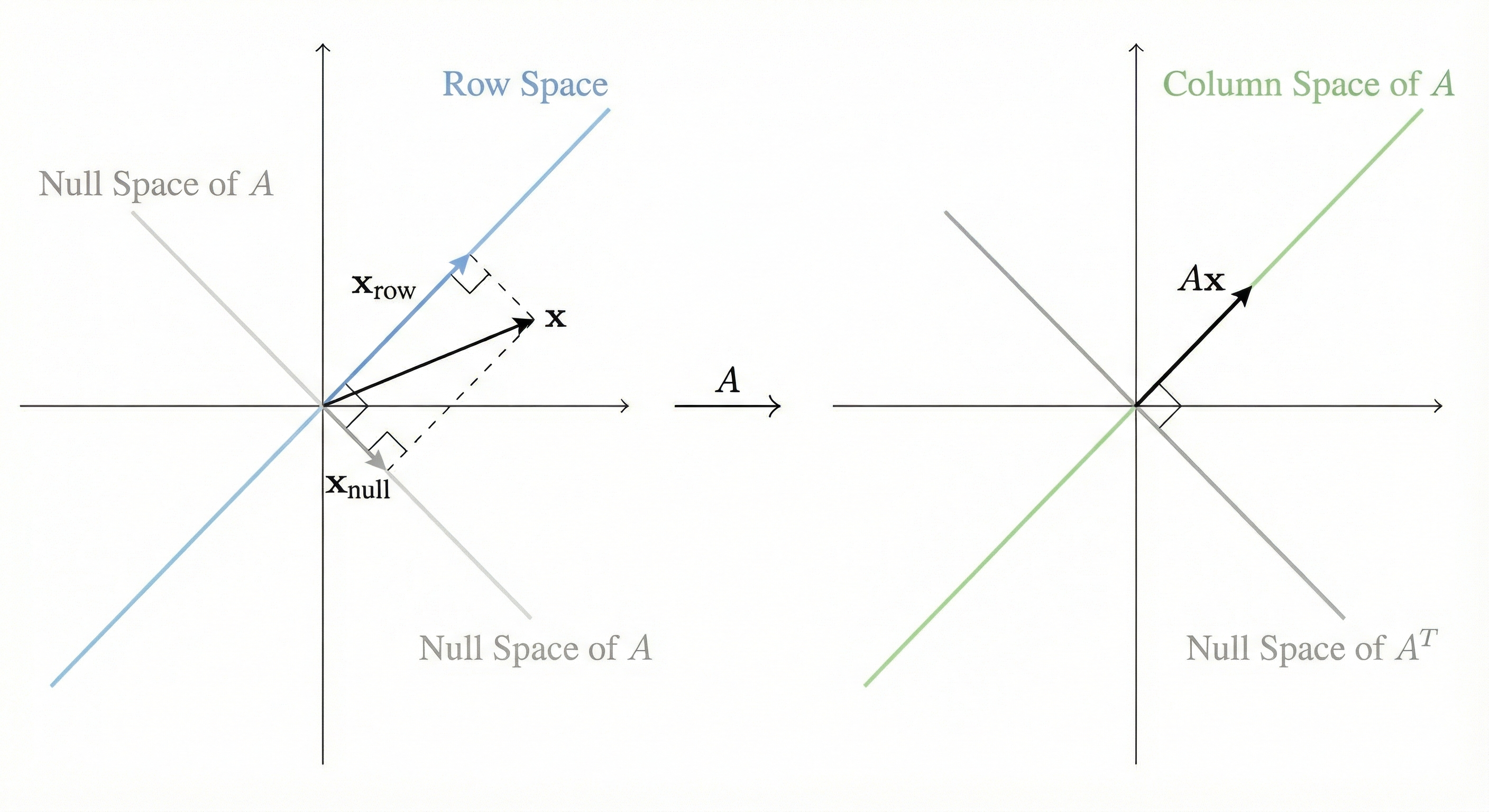 Figure: A rank-1 matrix maps the entire 2D input space onto a 1D line (the column space).
Figure: A rank-1 matrix maps the entire 2D input space onto a 1D line (the column space).
Problem
\[ A = \begin{bmatrix} 4 & 3 \\ 8 & 6 \end{bmatrix} \]
Observations: - Rank: 1 (second row is \(2 \times\) first row) - Row space: all multiples of \([4, 3]\) - Column space: all multiples of \([4, 8]\) (or equivalently \([1, 2]\))
Step 1: Compute \(v_1\) (Normalize Row Space)
The row space is spanned by \([4, 3]\). Normalize:
\[ v_1 = \frac{1}{\sqrt{16 + 9}} \begin{bmatrix} 4 \\ 3 \end{bmatrix} = \frac{1}{5} \begin{bmatrix} 4 \\ 3 \end{bmatrix} \]
Step 2: Compute \(u_1\) (Normalize Column Space)
The column space is spanned by \([4, 8]\) or equivalently \([1, 2]\). Normalize:
\[ u_1 = \frac{1}{\sqrt{1 + 4}} \begin{bmatrix} 1 \\ 2 \end{bmatrix} = \frac{1}{\sqrt{5}} \begin{bmatrix} 1 \\ 2 \end{bmatrix} \]
Step 3: Compute \(\sigma_1\) via \(AA^{\top}\)
\[ AA^{\top} = \begin{bmatrix} 4 & 3 \\ 8 & 6 \end{bmatrix} \begin{bmatrix} 4 & 8 \\ 3 & 6 \end{bmatrix} = \begin{bmatrix} 25 & 50 \\ 50 & 100 \end{bmatrix} \]
Eigenvalues: Solve \(\det(AA^{\top} - \lambda I) = 0\):
\[ (25 - \lambda)(100 - \lambda) - 2500 = \lambda^2 - 125\lambda = 0 \]
So \(\lambda_1 = 125, \lambda_2 = 0\).
Singular value:
\[ \sigma_1 = \sqrt{125} = 5\sqrt{5} \]
Step 4: Complete \(V\) and \(U\) (Nullspace Vectors)
For \(V\): Need \(v_2 \perp v_1\), so:
\[ v_2 = \frac{1}{5} \begin{bmatrix} 3 \\ -4 \end{bmatrix} \]
For \(U\): Need \(u_2 \perp u_1\), so:
\[ u_2 = \frac{1}{\sqrt{5}} \begin{bmatrix} 2 \\ -1 \end{bmatrix} \]
Final SVD
\[ A = U\Sigma V^{\top} = \frac{1}{\sqrt{5}} \begin{bmatrix} 1 & 2 \\ 2 & -1 \end{bmatrix} \begin{bmatrix} 5\sqrt{5} & 0 \\ 0 & 0 \end{bmatrix} \frac{1}{5} \begin{bmatrix} 4 & 3 \\ 3 & -4 \end{bmatrix} \]
Note: \(\Sigma\) has a zero on the diagonal because \(\text{rank}(A) = 1\).
6. What Does SVD Tell Us? Geometric Interpretation
The SVD provides orthonormal bases for all four fundamental subspaces:
Row Space and Column Space (Active Part)
- \(v_1, v_2, \ldots, v_r\): orthonormal basis for row space of \(A\)
- \(u_1, u_2, \ldots, u_r\): orthonormal basis for column space of \(A\)
The matrix \(A\) maps each \(v_i\) to \(\sigma_i u_i\):
\[ Av_i = \sigma_i u_i \]
The singular values \(\sigma_i\) measure how much \(A\) stretches along each direction.
Nullspaces (Inactive Part)
- \(v_{r+1}, \ldots, v_n\): orthonormal basis for nullspace of \(A\)
- \(u_{r+1}, \ldots, u_m\): orthonormal basis for left nullspace (nullspace of \(A^{\top}\))
These vectors get mapped to zero:
\[ Av_i = 0 \quad \text{for } i > r \]
Complete Picture
\[ \underbrace{\begin{bmatrix} | & | & & | & | & & | \\ u_1 & u_2 & \cdots & u_r & u_{r+1} & \cdots & u_m \\ | & | & & | & | & & | \end{bmatrix}}_{U \text{ (column space)} \oplus \text{(left null)}} \underbrace{\begin{bmatrix} \sigma_1 & & & & \\ & \ddots & & & \\ & & \sigma_r & & \\ & & & 0 & \\ & & & & \ddots \end{bmatrix}}_{\Sigma} \underbrace{\begin{bmatrix} - & v_1^{\top} & - \\ & \vdots & \\ - & v_r^{\top} & - \\ - & v_{r+1}^{\top} & - \\ & \vdots & \\ - & v_n^{\top} & - \end{bmatrix}}_{V^{\top} \text{ (row space)} \oplus \text{(null)}} \]
Key insight: SVD gives the best orthonormal coordinates for understanding how \(A\) transforms space: - Input coordinates: \(v_i\) (rows of \(V^{\top}\)) - Output coordinates: \(u_i\) (columns of \(U\)) - Scaling factors: \(\sigma_i\) (diagonal of \(\Sigma\))
Summary
| Concept | Description |
|---|---|
| SVD Formula | \(A = U\Sigma V^{\top}\) |
| \(U\) | \(m \times m\) orthogonal matrix; columns are left singular vectors (basis for column space ⊕ left nullspace) |
| \(\Sigma\) | \(m \times n\) diagonal matrix; diagonal entries are singular values \(\sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r > 0\) |
| \(V\) | \(n \times n\) orthogonal matrix; columns are right singular vectors (basis for row space ⊕ nullspace) |
| Computing \(V, \sigma^2\) | Eigenvectors and eigenvalues of \(A^{\top}A\) |
| Computing \(U, \sigma^2\) | Eigenvectors and eigenvalues of \(AA^{\top}\) |
| Rank | Number of nonzero singular values |
| Geometric meaning | \(A\) maps orthonormal basis \(v_i\) to scaled orthonormal basis \(\sigma_i u_i\) |
Why SVD is important: - Unique (up to sign and ordering of singular values) - Always exists (for any matrix, even non-square or singular) - Numerically stable computation - Applications: dimensionality reduction (PCA), image compression, least squares, pseudoinverse, matrix approximation