MIT 18.06 Lecture 15: Projection onto Subspaces
1. Projection of a Vector onto a Line
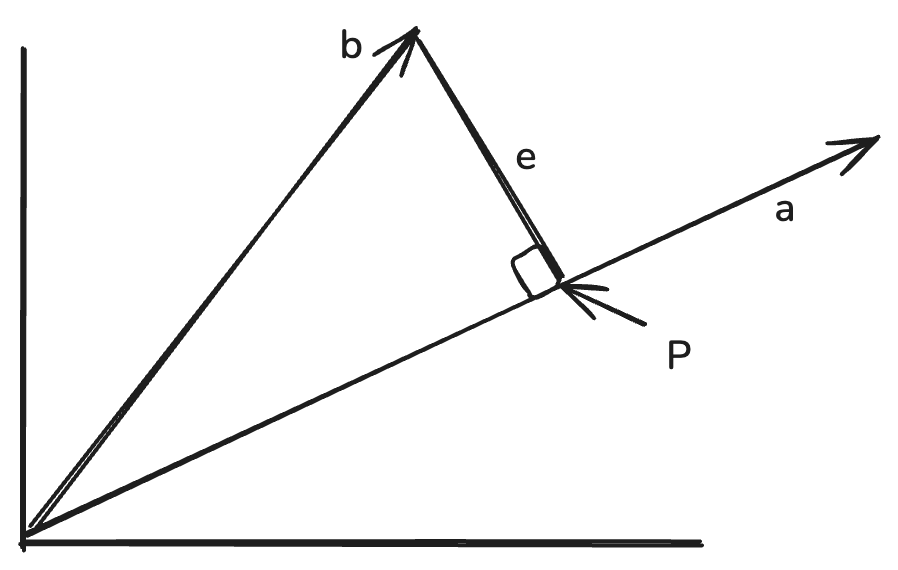
Setup: Project vector \(b\) onto vector \(a\).
Key equations:
\[ \begin{aligned} p &= xa \\ a^T(b - xa) &= 0 \\ a^T b &= xa^T a \\ x &= \frac{a^T b}{a^T a} \end{aligned} \]
Components:
- \(p\): Projection of \(b\) onto \(a\)
- \(e\): Error vector
- \(e \perp a\) (error is perpendicular to \(a\))
Key relationships:
\[ e = b - p \]
\[ p + e = b \]
\[ p = b - e \]
Projection formula:
\[ p = a\frac{a^T b}{a^T a} \]
Properties: - If \(b\) is doubled, then \(p\) is doubled - If \(a\) is doubled, then \(p\) does not change at all
2. Projection Matrix
Matrix form:
\[ p = Pb \]
where
\[ P = \frac{aa^T}{a^T a} \]
Analysis:
The projection matrix \(P = \frac{aa^T}{a^T a}\) has these properties:
- The numerator \(aa^T\) is \((n \times 1)(1 \times n) = n \times n\)
- The denominator \(a^T a\) is a scalar
- Therefore \(P\) is \(n \times n\)
- Column space of \(P\) is the line through \(a\)
- Rank is 1
- Symmetric: \(P^T = P\)
- Idempotent: \(P^2 = P\) (if I project twice, the result is the same)
3. Why Projection?
Problem: The equation \(Ax = b\) may have 0 solutions when \(m > n\).
Solution: Solve \(A\hat{x} = p\) instead, where \(p\) is the projection of \(b\) onto the column space.
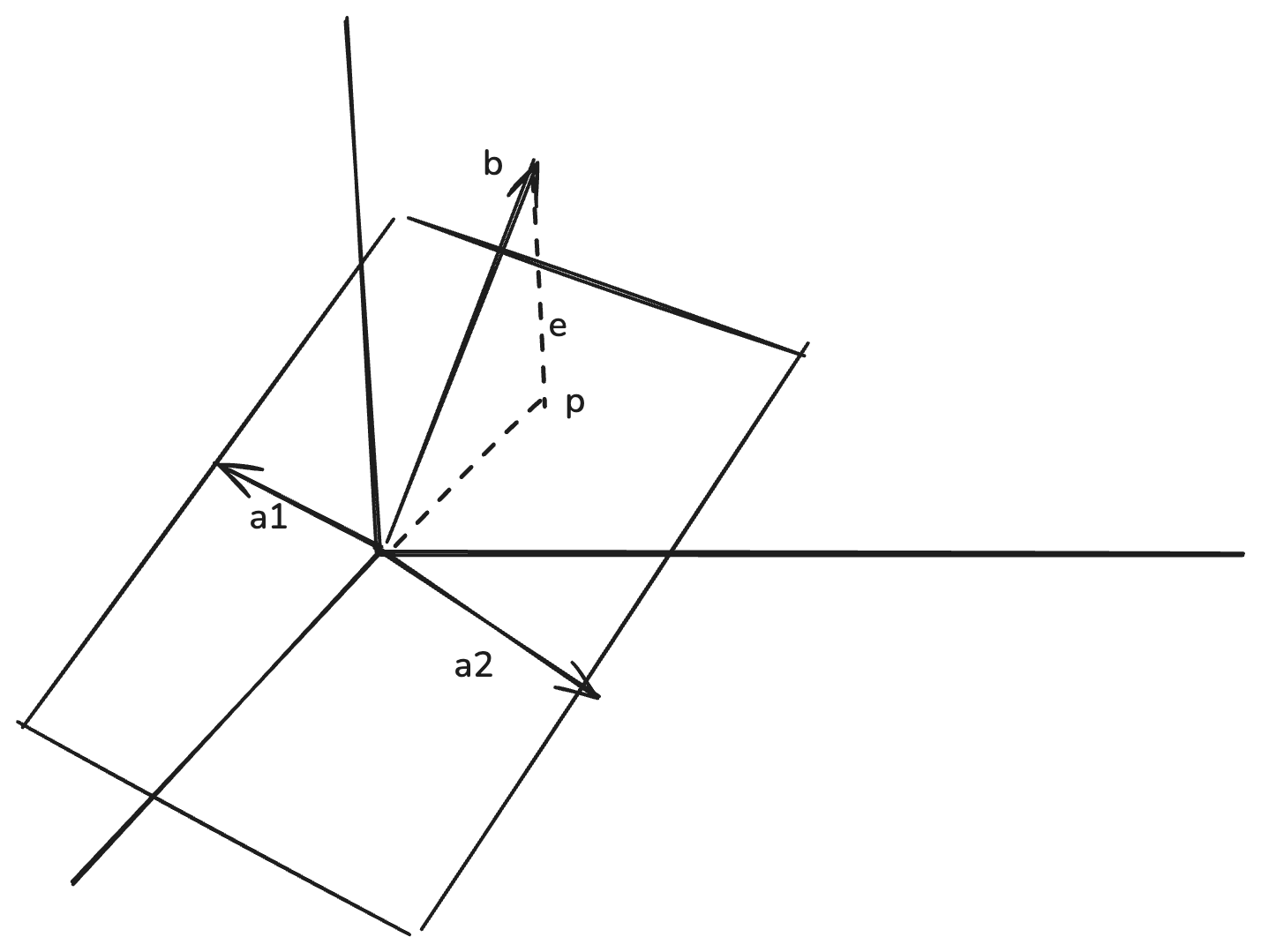
Setup:
The error \(e = b - p\) is perpendicular to the plane (spanned by \(a_1\) and \(a_2\)).
\[ A = \begin{bmatrix}| & | \\ a_1 & a_2 \\ | & |\end{bmatrix} \]
\[ p = \hat{x}_1 a_1 + \hat{x}_2 a_2 = A\hat{x} \]
4. Finding \(\hat{x}\)
Key idea: \(b - A\hat{x} \perp C(A)\) (error is perpendicular to column space)
Derivation: Error \(e\) is perpendicular to \(a_1\) and \(a_2\):
\[ \begin{aligned} a_1^T(b - A\hat{x}) &= 0 \text{ and } a_2^T(b - A\hat{x}) = 0 \\ \begin{bmatrix}a_1^T \\ a_2^T\end{bmatrix}(b - A\hat{x}) &= \begin{bmatrix}0 \\ 0\end{bmatrix} \\ A^T(b - A\hat{x}) &= \mathbf{0} \end{aligned} \]
Key relationships:
The error \(e = b - A\hat{x}\) is in the left null space:
\[ e \in N(A^T) \]
\[ e \perp C(A) \]
This means the error is perpendicular to the column space of \(A\).
Normal equations:
\[ A^T b = A^T A\hat{x} \]
Solution:
\[ \hat{x} = (A^T A)^{-1} A^T b \]
Projection:
\[ p = A\hat{x} = A(A^T A)^{-1} A^T b \]
Projection matrix:
\[ P = A(A^T A)^{-1} A^T \]
Special case: If \(A\) is invertible, then \(P = I\) (identity matrix).
Properties in high dimensions: - \(P^T = P\) (symmetric) - \(P^2 = P\) (idempotent)
5. Least Squares Application
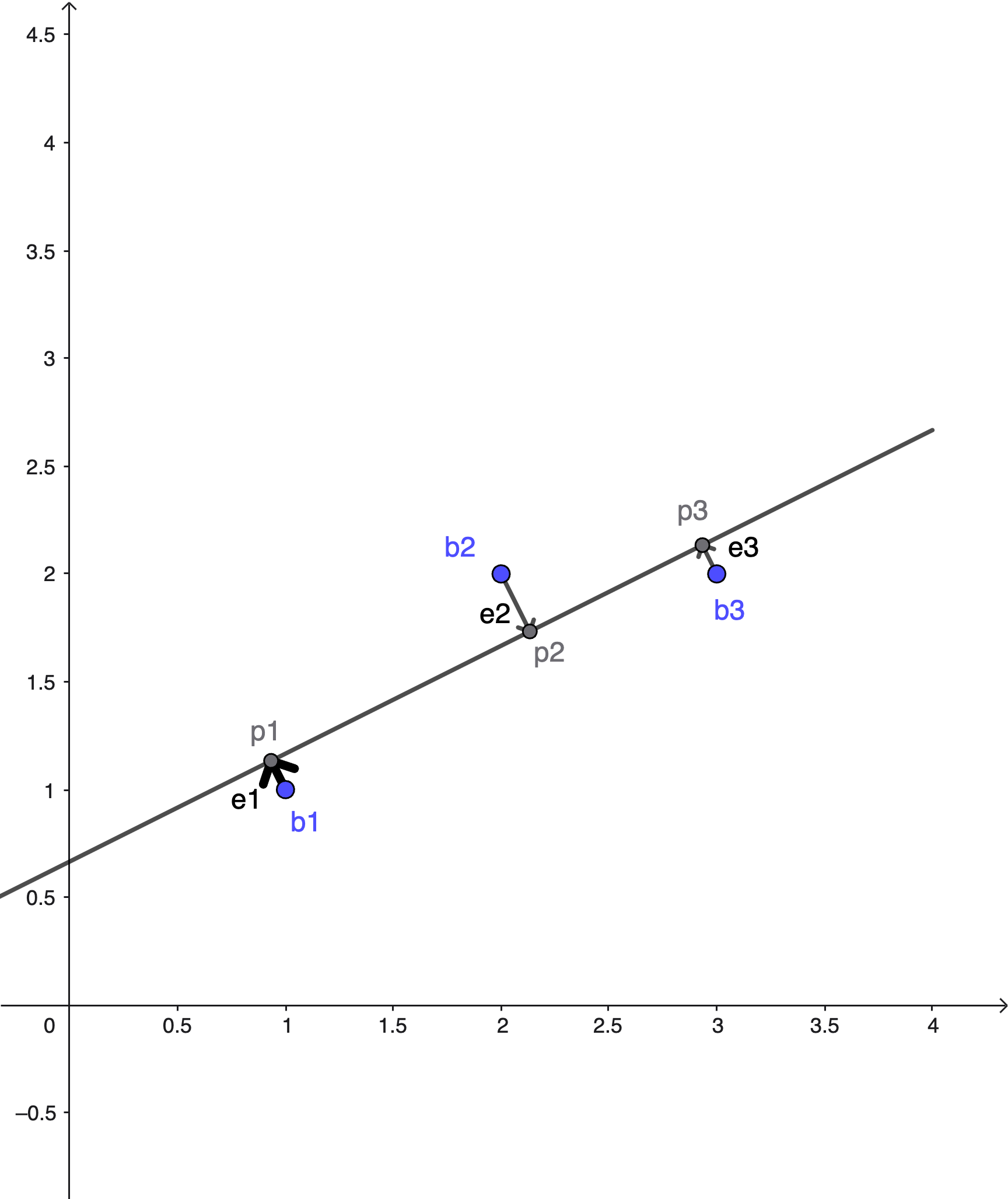
Problem: Fit a line \(y = c + dt\) to data points \((1,1)\), \((2,2)\), and \((3,3)\).
Setup:
\[ A = \begin{bmatrix} 1 & 1 \\ 1 & 2 \\ 1 & 3 \end{bmatrix}, \quad b = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}, \quad x = \begin{bmatrix} c \\ d \end{bmatrix} \]
Equation system: \(Ax = b\) - Row 1: \(c + 1 \cdot d = 1\) - Row 2: \(c + 2 \cdot d = 2\) - Row 3: \(c + 3 \cdot d = 3\)
Issue: Cannot find exact solution for \(x\) because: - \(A\) is not invertible (not square: \(3 \times 2\)) - System is overdetermined (3 equations, 2 unknowns)
Solution: Use projection to find \(\hat{x}\) that minimizes \(\|Ax - b\|^2\).
6. Geometric Interpretation
3 Lines in 3D: If we have 3 lines in 3-dimensional space, then \(A\) will be square.
If \(A\) is invertible (full rank): - \(Ax = b\) has an exact solution - The solution geometrically means: find the plane spanned by column 1 and column 2, then find where column 3 crosses it
Source: MIT 18.06SC Linear Algebra, Lecture 15