Goodfellow Deep Learning — Deep Learning Chapter 7.14: Tangent Distance, Tangent Prop and Manifold Tangent Classifier
The Manifold Assumption
The assumption is that samples lie on a low-dimensional manifold embedded in a high-dimensional space.
If we measure their distance using the Euclidean metric, the points might appear far apart, even though they actually reside on the same manifold.
Tangent Distance: Difficulties and Alternative
The Challenge
Computing tangent distances directly is computationally expensive. For every pair of samples, it requires solving an optimization problem to find the minimal distance between two tangent planes that approximate their local manifolds. This becomes infeasible with large datasets or high-dimensional input spaces.
The Alternative
As an alternative, the method approximates the manifold locally using the tangent plane at a single point. Instead of explicitly finding the closest points between two manifolds, we measure distances using these local linear approximations. This greatly reduces computational cost while still capturing local invariance properties.
Tangent Prop
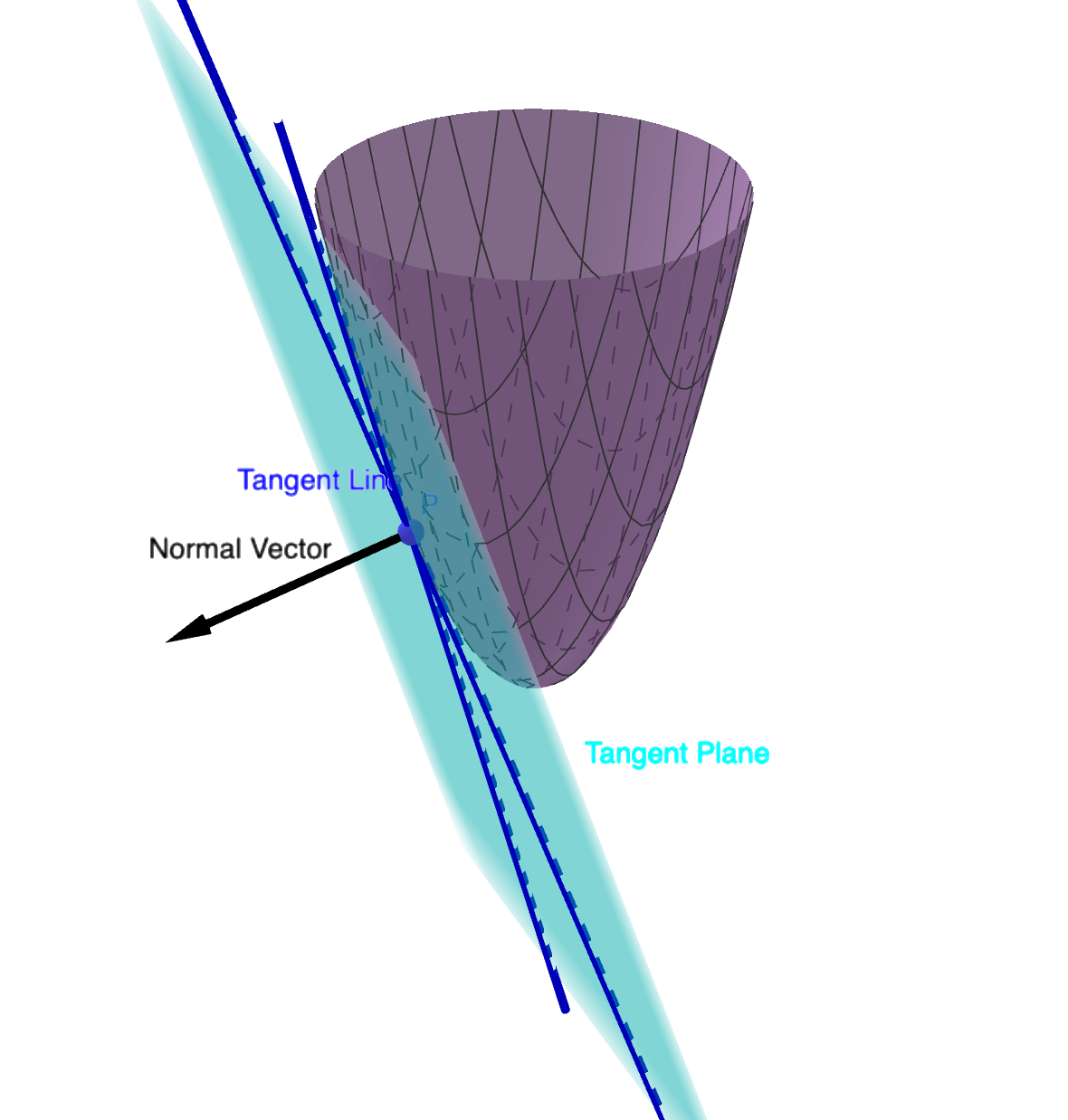
The figure illustrates how Tangent Propagation enforces local invariance of the model output along the tangent directions of the data manifold.
Each data point lies on a smooth low-dimensional surface embedded in high-dimensional space. The tangent plane represents all directions along which the data can move without changing its semantic meaning (e.g., small translation or rotation).
The normal vector points in the direction orthogonal to the manifold — changes along this direction correspond to changes in class or semantic meaning.
This approach achieves partial consistency by forcing \(\nabla_xf(x) \perp v^{(i)}\).
Regularization Term
\[ \Omega(f)=\sum_i\left((\nabla_xf(x)^\top v^{(i)})^2\right) \]
This regularization term penalizes the sensitivity of the network’s output \(f(x)\) to small movements along each tangent direction \(v^{(i)}\).
Minimizing this term encourages the model’s gradient \(\nabla_x f(x)\) to be orthogonal to all tangent vectors, ensuring that \(f(x)\) remains approximately constant when the input slides along the manifold.
In short: Tangent Propagation achieves local smoothness along the manifold (invariance to small deformations), while still allowing sharp variation in directions orthogonal to the manifold, which separate different classes.
Tangent Direction Vectors
In Tangent Propagation, each \(v^{(i)}\) represents a tangent direction of the data manifold at the point \(x\).
It describes a small, meaningful variation of the input that should not change the output of the network—for example, a slight translation, rotation, or scaling of an image.
Mathematically, \(v^{(i)}\) can be obtained as the derivative of a transformation \(T(x, \alpha_i)\) with respect to its parameter:
\[ v^{(i)} = \left.\frac{\partial T(x, \alpha_i)}{\partial \alpha_i}\right|_{\alpha_i=0} \]
During training, the model is penalized if its output changes along these directions, which enforces invariance and smoothness of \(f(x)\) along the manifold.
From Tangent Propagation to Manifold Learning
Tangent Propagation regularizes the model so that its output remains invariant along directions of known transformations, such as translations or rotations.
It can be seen as an analytical version of data augmentation—rather than generating new samples, it directly penalizes the model’s sensitivity to those transformations.
Connections to Other Methods
This idea connects to bidirectional propagation and adversarial training, both of which encourage the model to stay locally smooth in input space.
Adversarial training extends Tangent Propagation by finding, for each input, the direction that most changes the model’s prediction and then enforcing robustness along that direction.
The Manifold Tangent Classifier (Rifai et al., 2011d) further removes the need to explicitly specify tangent directions.
It uses an autoencoder to learn the manifold structure and derive tangent vectors automatically, allowing the network to regularize itself along the data manifold without handcrafted transformations.
Manual Specification of Tangent Directions
A key limitation of Tangent Propagation is that these tangent directions \(v^{(i)}\) must be manually specified based on prior knowledge about the task.
For example, in handwritten digit recognition, we explicitly define directions corresponding to translation or rotation.
While this makes the method interpretable, it also limits its applicability—manual definitions are impractical for complex, high-dimensional data.
Source: Deep Learning (Ian Goodfellow, Yoshua Bengio, Aaron Courville) - Chapter 7.14