Lecture 33: Left and Right Inverse; Pseudo-inverse

Linear Algebra
MIT 18.06
Matrix Inverse
SVD
Pseudo-inverse
Author

Chao Ma

Published

November 26, 2025

Overview

This lecture explores inverses for non-square and singular matrices:

  • Two-sided inverse for square full-rank matrices
  • Why rectangular matrices cannot have two-sided inverses
  • Left inverse for full column rank matrices
  • Right inverse for full row rank matrices
  • Pseudo-inverse using SVD for singular matrices

1. Two-Sided Inverse

For a square matrix with full rank, we have a two-sided inverse:

\[ AA^{-1} = I = A^{-1}A \]

Requirements: \(r = m = n\) (A is full rank)

Uniqueness: The two-sided inverse is unique when it exists.

2. Rectangular Matrices

Key fact: Rectangular matrices cannot have a two-sided inverse.

Reason: Rectangular matrices must have either a nullspace or a left nullspace (or both), preventing a true two-sided inverse from existing.

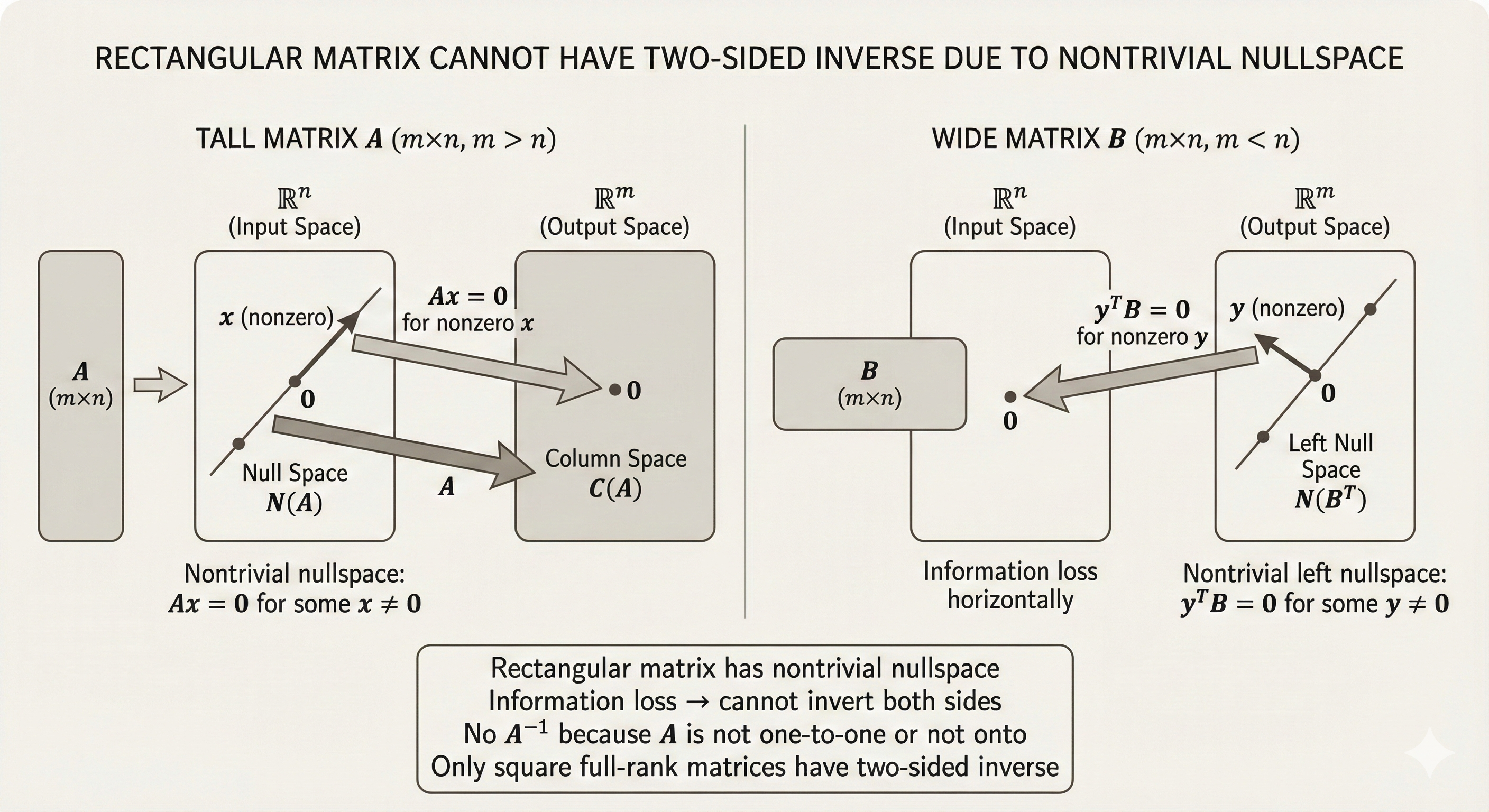Rectangular matrix inverses Figure: Rectangular matrices have one-sided inverses depending on their rank - full column rank matrices have left inverses, while full row rank matrices have right inverses.

Intuition: - If \(m > n\) (tall matrix): nullspace of \(A^T\) is non-empty - If \(m < n\) (wide matrix): nullspace of \(A\) is non-empty - Either way, information is lost in one direction

3. Left Inverse

For a full column rank matrix (\(r = n < m\)):

Properties

  • Rank: \(r = n\) (full column rank)
  • Nullspace: \(\text{null}(A) = \{0\}\) (only the zero vector)
  • Columns: All columns are independent
  • Solutions to \(Ax = b\): Either 0 or 1 solution (never infinite solutions)
  • \(A^T A\): Invertible (\(n \times n\) matrix)

Left Inverse Formula

\[ (A^T A)^{-1} A^T A = I \]

Therefore:

\[ A_{\text{left}}^{-1} = (A^T A)^{-1} A^T \]

Verification:

\[ A_{\text{left}}^{-1} A = (A^T A)^{-1} A^T A = I_n \]

Note: We get \(I_n\) (the \(n \times n\) identity), not \(I_m\).

Why \(A^T A\) Is Invertible

If \((A^T A)x = 0\), then:

\[ x^T (A^T A) x = 0 \implies (Ax)^T (Ax) = 0 \implies \|Ax\|^2 = 0 \]

Since \(A\) has full column rank, \(Ax = 0\) only when \(x = 0\).

Therefore, \(A^T A\) has trivial nullspace and is invertible.

4. Right Inverse

For a full row rank matrix (\(r = m < n\)):

Properties

  • Rank: \(r = m\) (full row rank)
  • Left nullspace: \(\text{null}(A^T) = \{0\}\)
  • Pivots: \(m\) pivots
  • Free variables: \(n - m\) free variables
  • Solutions to \(Ax = b\): Infinite solutions (when solution exists)
  • \(AA^T\): Invertible (\(m \times m\) matrix)

Right Inverse Formula

We want to find \(B\) such that:

\[ AB = I_m \]

Since \(AA^T\) is invertible:

\[ AA^T (AA^T)^{-1} = I_m \]

Therefore:

\[ A_{\text{right}}^{-1} = A^T (AA^T)^{-1} \]

Verification:

\[ A A_{\text{right}}^{-1} = A A^T (AA^T)^{-1} = I_m \]

5. Revisit \(Ax = b\)

Understanding the Mapping

  • Input: \(x \in \mathbb{R}^n\)
  • Output: \(Ax\) is a linear combination of columns, so \(Ax \in \mathbb{R}^m\)
  • Range: Output is in the column space of \(A\)

When Is \(A\) Invertible on the Row Space?

Claim: If \(x, y\) are both in the row space and \(x \neq y\), then \(Ax \neq Ay\) when \(A\) has full rank.

Proof

Assume \(Ax = Ay\) for \(x \neq y\) in the row space.

Then:

\[ A(x - y) = 0 \]

This means: - \(x - y\) is in the nullspace of \(A\) - \(x - y\) is in the row space (since it’s a combination of \(x\) and \(y\))

But the nullspace and row space are orthogonal complements, so:

\[ x - y \in \text{null}(A) \cap \text{row}(A) = \{0\} \]

Therefore \(x - y = 0\), which contradicts \(x \neq y\).

Conclusion: \(A\) is one-to-one (injective) when restricted to its row space.

6. Pseudo-Inverse

The pseudo-inverse provides a general way to “invert” singular or rectangular matrices.

Cases Where Pseudo-Inverse Is Useful

  1. \(r = n, r < m\) (full column rank, tall matrix)
  2. \(r = m, r < n\) (full row rank, wide matrix)
  3. \(r < m, r < n\) (rank deficient in both dimensions)

Computing \(A^+\) Using SVD

From the Singular Value Decomposition:

\[ A = U \Sigma V^T \]

The pseudo-inverse is:

\[ A^+ = V \Sigma^+ U^T \]

where \(\Sigma^+\) is the pseudo-inverse of the diagonal matrix \(\Sigma\).

Constructing \(\Sigma^+\)

If \(\Sigma\) is an \(m \times n\) diagonal matrix with singular values \(\sigma_1, \sigma_2, \ldots, \sigma_r\):

\[ \Sigma = \begin{bmatrix} \sigma_1 & 0 & 0 & \cdots & 0 \\ 0 & \sigma_2 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 0 \end{bmatrix}_{m \times n} \]

Then \(\Sigma^+\) is the \(n \times m\) matrix:

\[ \Sigma^+ = \begin{bmatrix} \frac{1}{\sigma_1} & 0 & 0 & \cdots & 0 \\ 0 & \frac{1}{\sigma_2} & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 0 \end{bmatrix}_{n \times m} \]

Construction rule: - Take reciprocals of non-zero singular values: \(\sigma_i \to \frac{1}{\sigma_i}\) - Keep zeros as zeros - Transpose the shape: \(m \times n \to n \times m\)

Properties of Pseudo-Inverse

  1. Reduces to regular inverse when \(A\) is invertible: If \(A\) is square and full rank, \(A^+ = A^{-1}\)

  2. Reduces to left inverse: If \(A\) has full column rank, \(A^+ = (A^T A)^{-1} A^T\)

  3. Reduces to right inverse: If \(A\) has full row rank, \(A^+ = A^T (AA^T)^{-1}\)

  4. Moore-Penrose conditions: \(A^+\) is the unique matrix satisfying:

    • \(A A^+ A = A\)
    • \(A^+ A A^+ = A^+\)
    • \((A A^+)^T = A A^+\)
    • \((A^+ A)^T = A^+ A\)

Summary

Matrix Type Rank Inverse Type Formula
Square full rank \(r = m = n\) Two-sided \(A^{-1}\)
Tall full column rank \(r = n < m\) Left inverse \((A^T A)^{-1} A^T\)
Wide full row rank \(r = m < n\) Right inverse \(A^T (AA^T)^{-1}\)
Rank deficient \(r < \min(m,n)\) Pseudo-inverse \(V \Sigma^+ U^T\)

Key insights: - Rectangular matrices cannot have two-sided inverses - One-sided inverses exist when the matrix has full rank in one dimension - The pseudo-inverse generalizes all these cases using SVD - The pseudo-inverse always exists, even for singular matrices