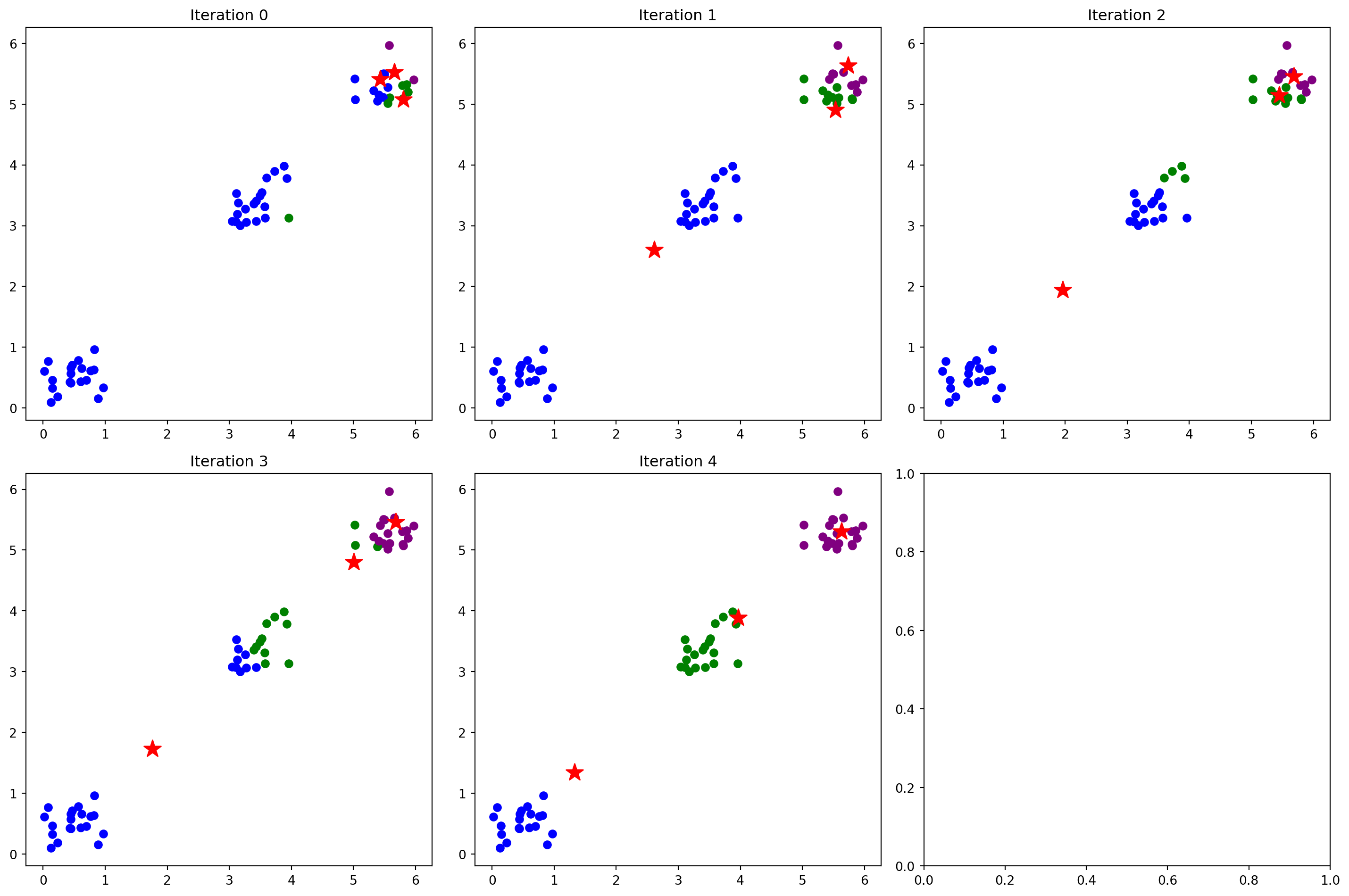
K-means Clustering

Setup points and K

we will implement a KNN algorithm to cluster the points

X=[[1,1],[2,2.1],[3,2.5],[6,7],[7,7.1],[9,7.5]]
k=2

max_iter=3

# Visualize the data


import matplotlib.pyplot as plt

plt.scatter([x[0] for x in X],[x[1] for x in X])
plt.show()

# Pure python implementation of K-means clustering
def knn_iter(X,centroids):
    # set up new clusters
    new_clusters=[[] for _ in range(len(centroids))]
    # k=len(centroids)
    # assign each point to the nearest centroid
    for x in X:
        k,distance=0,(x[0]-centroids[0][0])**2+(x[1]-centroids[0][1])**2
        for i,c in enumerate(centroids[1:],1):
            if (x[0]-c[0])**2+(x[1]-c[1])**2<distance:
                k=i
                distance=(x[0]-c[0])**2+(x[1]-c[1])**2
        new_clusters[k].append(x)
    
    # calculate new centroids
    new_centroids=[[
        sum([x[0] for x in cluster])/len(cluster),
        sum([x[1] for x in cluster])/len(cluster)
    ] if cluster else centroids[i] for i,cluster in enumerate(new_clusters)]
    return new_centroids

def iter_and_draw(X,k,max_iter):
    centroids=X[:k]  # Randomly select 2 centroids
    fig, axes = plt.subplots(max_iter//3+(1 if max_iter%3!=0 else 0),
        3, figsize=(15, 10))
    axes=axes.flatten()
    for i in range(max_iter):
        
        # Plot points and centroids


        # Assign each point to nearest centroid and plot with corresponding color
        colors = ['blue', 'green', 'purple', 'orange', 'brown', 'pink', 'gray', 'olive', 'cyan']
        for j, x in enumerate(X):
            # Find nearest centroid
            min_dist = float('inf')
            nearest_centroid = 0
            for k, c in enumerate(centroids):
                dist = (x[0]-c[0])**2 + (x[1]-c[1])**2
                if dist < min_dist:
                    min_dist = dist
                    nearest_centroid = k
            # Plot point with color corresponding to its cluster
            axes[i].scatter(x[0], x[1], c=colors[nearest_centroid % len(colors)], label=f'Cluster {nearest_centroid+1}' if j==0 else "")
        axes[i].scatter([c[0] for c in centroids], [c[1] for c in centroids], c='red', marker='*', s=200, label='Centroids')
        axes[i].set_title(f'Iteration {i}')
        centroids = knn_iter(X, centroids)

    plt.tight_layout()
    plt.show()

iter_and_draw(X,k,max_iter)
# print(centroids)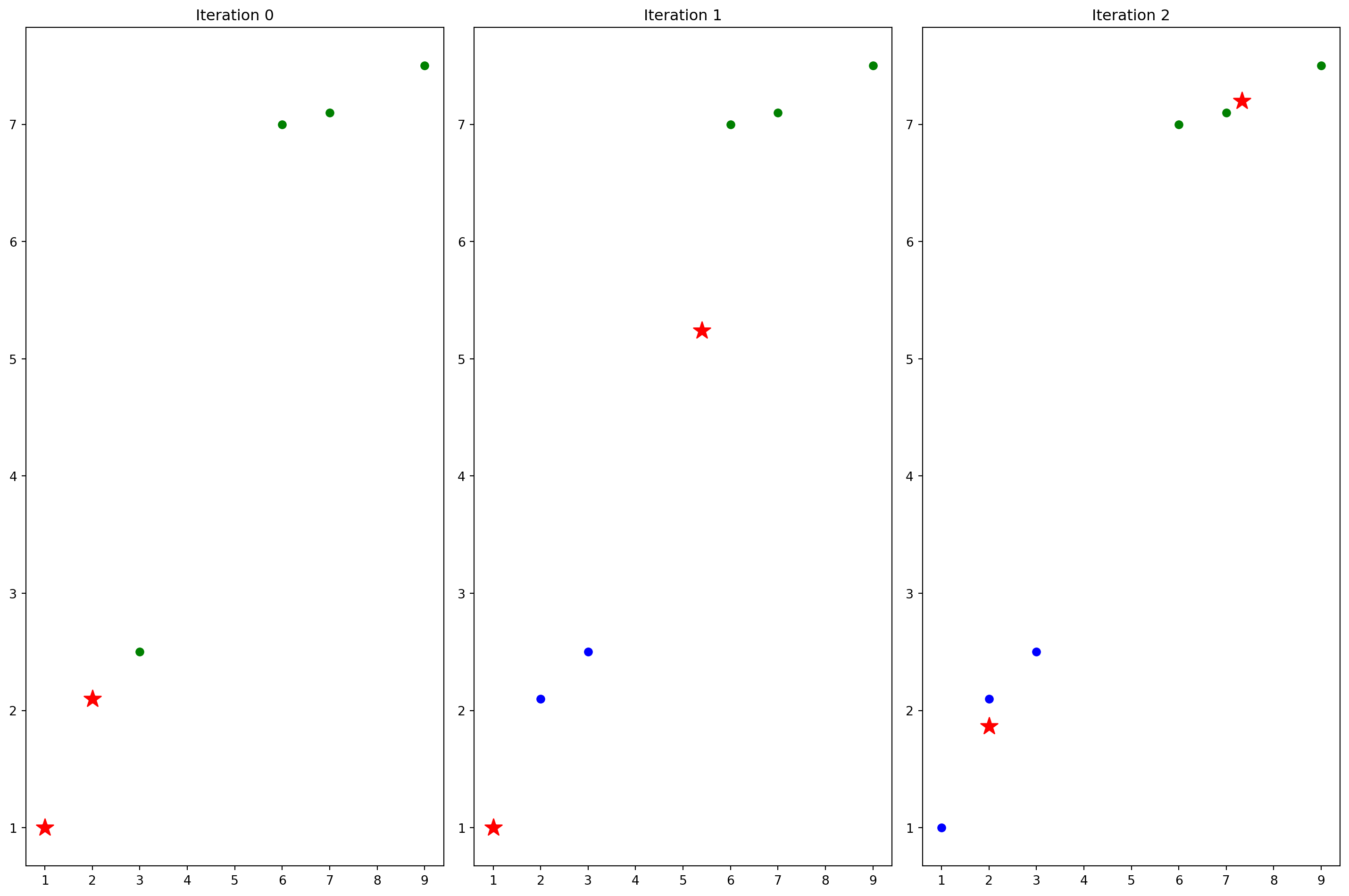

# A 3 clusters example

import numpy as np

X1=np.random.rand(20,2)+5 # Some points in the upper right corner
X2=np.random.rand(20,2)+3 # Some points in the middle
X3=np.random.rand(20,2) # Some points in the lower left corner

iter_and_draw(np.concatenate((X1,X2,X3)),3,5)

A question?

• What to do if one cluster has no assigned points during iteration?

Formula Derivation

The goal is to minimize the loss of inertia which is sum of the points to cluster centroids.

\[ Loss= \sum_{i=1}^n \sum_{x \in C_i} ||x-\mu_i||^2 \]

To iter \(\mu\) for each cluster, let us find the derivative of the following function. \[ f(\mu)=\sum_{i=1}^n ||x_i-\mu||^2 = \sum_{i=1}^n {x_i}^2+\mu^2-2x_i\mu \]

Given a \(\nabla \mu\), \[ f(\mu + \nabla \mu)=\sum_{i=1}^n ||x_i+\nabla \mu -\mu||^2 = \sum_{i=1}^n {x_i}^2+\mu^2+{\nabla \mu}^2-2{x_i \mu}-2{\mu \nabla \mu}+2{x_i \nabla \mu} \]

\[ f(\mu + \nabla \mu)-f(\mu)= \sum_{i=1}^n {\nabla \mu}^2-2{\mu \nabla \mu}+2{x_i \nabla \mu} \]

\[ \frac {f(\mu + \nabla \mu)-f(\mu)}{\nabla \mu}=\sum_{i=1}^n {\nabla \mu} -2 \mu +2{x_i} = 2\sum_{i=1}^n x_i - 2n\mu \]

Now we can see if \(n\mu = \sum_{i=1}^n x_i\), then the derivative is 0, this is why in each iteration, we need to set the center of the cluster as centroid.