MIT 18.06 Lecture 17: Orthogonal Matrices and Gram-Schmidt
Orthonormal Vectors
Orthonormal vectors are perpendicular to each other and have unit length.
\[ q_i^\top q_j=\begin{cases}0 & \text{if }i\ne j,\\1&\text{if }i=j\end{cases} \]
This means:
- \(q_i \perp q_j\) if \(i\neq j\) (orthogonal)
- \(\|q_i\|^2=1 \: \forall i \in \{1,2...n\}\) (normalized)
Orthonormal Matrices
A matrix \(Q\) with orthonormal columns satisfies \(Q^\top Q=I_n\).
\[ Q^\top Q=I_n \]
If \(Q\) is square, then \(Q^\top=Q^{-1}\) (the transpose equals the inverse).
Examples of Orthonormal Matrices
Permutation Matrices:
\[ Q=\begin{bmatrix}0&0&1\\1&0&0\\0&1&0\end{bmatrix} \]
Rotation Matrix:
\[ Q=\begin{bmatrix}\cos\theta&-\sin\theta\\ \sin\theta&\cos\theta \end{bmatrix} \]
Hadamard Matrix:
\[ Q=\frac{1}{\sqrt{2}}\begin{bmatrix}1&1\\1&-1\end{bmatrix} \]
\[ Q=\frac{1}{2}\begin{bmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\end{bmatrix} \]
Projection onto Orthonormal Matrices
When \(Q\) has orthonormal columns, the projection matrix simplifies significantly.
\[ P=Q(Q^\top Q)^{-1}Q^\top=QQ^\top \]
If \(Q\) is square: \(P=I\)
Proof of the 2 key properties:
- Symmetric: \(QQ^\top\) is symmetric
- Idempotent:
\[ (QQ^\top)(QQ^\top)=QIQ^\top=QQ^\top \]
Least squares simplification:
General form:
\[ A^\top A\hat{x}=A^\top b \]
If \(A\) is an orthonormal matrix \(Q\), the solution becomes trivial:
\[ \begin{aligned} Q^\top Q \hat{x} &= Q^\top b \\ \hat{x} &= Q^\top b \\ \hat{x}_i &= q_i^\top b \end{aligned} \]
Each component is simply the projection of \(b\) onto the corresponding column of \(Q\).
Gram-Schmidt Process
The Gram-Schmidt process converts independent vectors into orthonormal vectors.
Given 2 independent vectors \(a\) and \(b\):
- \(q_1=\frac{A}{\|A\|}\)
- \(q_2=\frac{B}{\|B\|}\)
2D Case
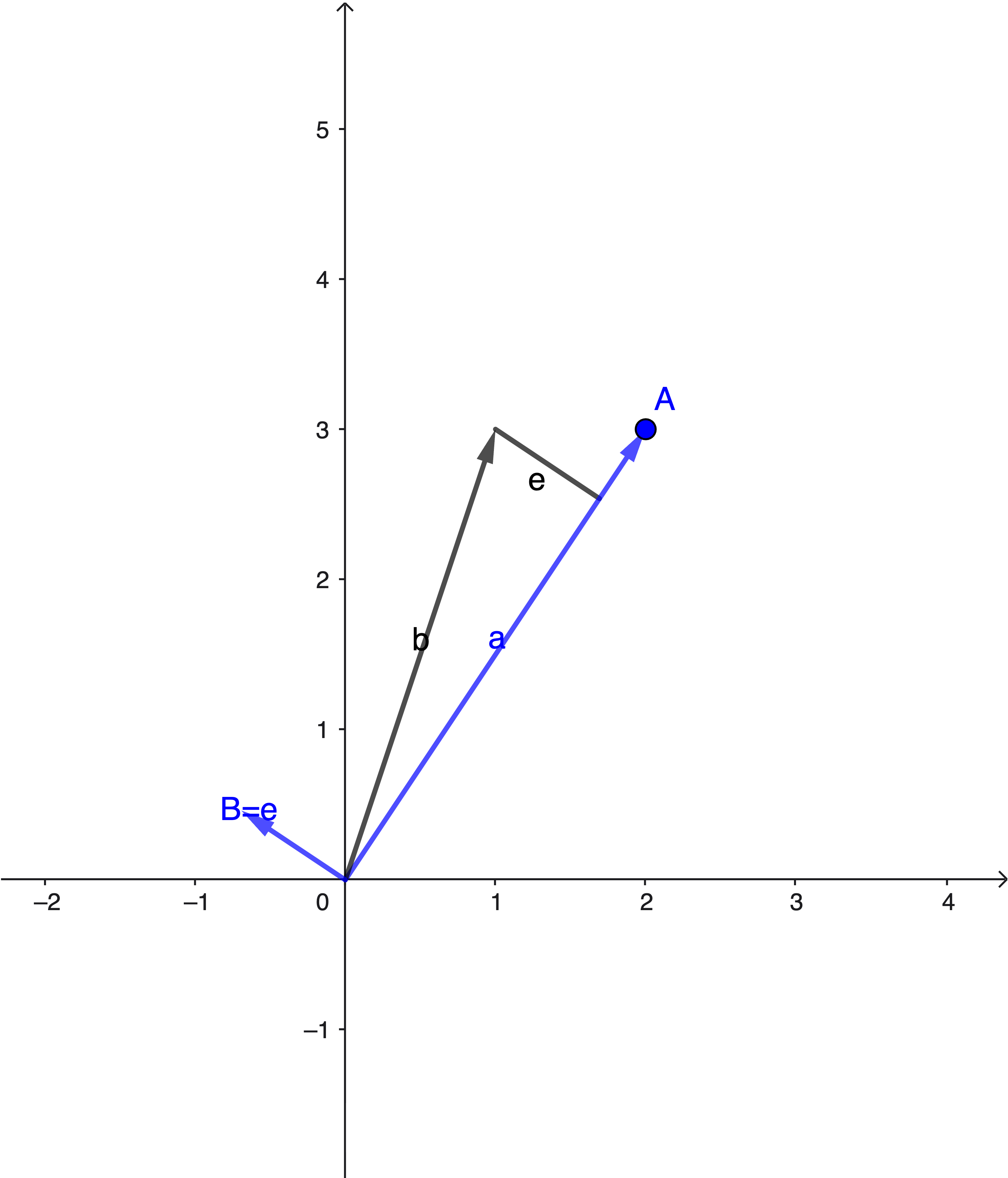
Set \(a\) as \(A\) (no change needed for the first vector).
We then remove the projection of \(b\) onto \(a\) from \(b\), using the error component as \(B\).
This ensures \(A \perp B\).
\[ B=b-\frac{A^\top b}{A^\top A}A \]
Proof:
\[ A^\top B=A^\top b-A^\top A\frac{A^\top b}{A^\top A}=0 \]
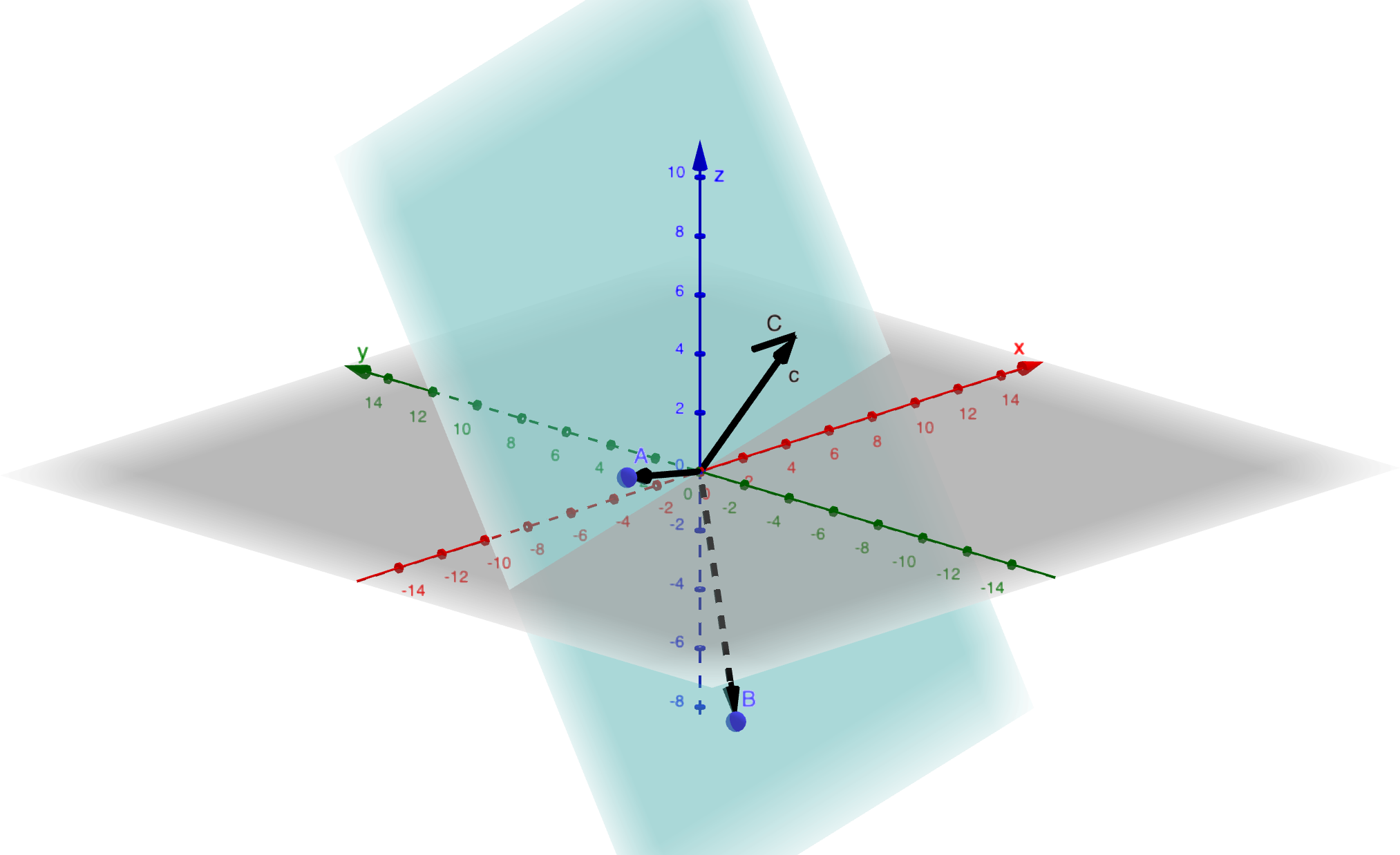
3D Case
At this point, we have orthogonal vectors \(A\) and \(B\), and we find \(C\) by removing its projections onto both \(A\) and \(B\).
\[ q_3=\frac{C}{\|C\|} \]
\[ C=c-\frac{A^\top c}{A^\top A}A-\frac{B^\top c}{B^\top B}B \]
\[ C \perp A \text{ and } C\perp B \]
Real Example
Given:
- \(a=\begin{bmatrix}1\\1\\1\end{bmatrix}\)
- \(b=\begin{bmatrix}1\\0\\2\end{bmatrix}\)
The original matrix \(M\) is:
\[ M=\begin{bmatrix}1&1\\1&0\\1&2\end{bmatrix} \]
Step 1: Use \(a\) as \(A\)
Step 2: Calculate \(B\):
\[ \begin{aligned} B &= b-\frac{A^\top b}{A^\top A}A \\ &= b-\frac{3}{3}A \\ &= \begin{bmatrix}0\\-1\\1\end{bmatrix} \end{aligned} \]
Step 3: Normalize to get \(Q\)
\(q_1\):
\[ \frac{1}{\sqrt{3}}\begin{bmatrix}1\\1\\1\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{3}}\\\frac{1}{\sqrt{3}}\\\frac{1}{\sqrt{3}}\end{bmatrix} \]
\(q_2\):
\[ \frac{1}{\sqrt{2}}\begin{bmatrix}0\\-1\\1\end{bmatrix}=\begin{bmatrix}0\\\frac{-1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{bmatrix} \]
Result:
\[ Q=\begin{bmatrix}\frac{1}{\sqrt{3}}&0\\\frac{1}{\sqrt{3}}&\frac{-1}{\sqrt{2}}\\\frac{1}{\sqrt{3}}&\frac{1}{\sqrt{2}}\end{bmatrix} \]
QR Factorization
\(Q\) spans the same column space as \(M\), so we can write \(M=QR\).
- \(Q\) is \(m \times n\) (orthonormal columns)
- \(R\) is \(n \times n\) (upper triangular)
Because \(Q\) is orthonormal:
\[ Q^\top M=R \]
\[ r_{ij}=q_i^\top m_j \]
Why is R upper triangular?
\[ \begin{bmatrix}|&|\\a_1&a_2\\|&|\end{bmatrix}=\begin{bmatrix}q_1&q_2\end{bmatrix}\begin{bmatrix}a_1^\top q_1&a_2^\top q_1\\0 &a_2^\top q_2\end{bmatrix} \]
Because \(q_1 \perp q_2\), we have \(q_2^\top a_1=0\) in the lower left position, making \(R\) upper triangular.
Source: MIT 18.06SC Linear Algebra, Lecture 17