Show code
import numpy as np
import matplotlib.pyplot as plt
from typing import Tuple
# Set random seed for reproducibility
np.random.seed(42)
print("✓ Setup complete")✓ Setup completeChao Ma
October 2, 2025
This recap of Deep Learning Chapter 6.5 explores backpropagation—the algorithm that makes training deep neural networks computationally feasible by efficiently computing gradients through the chain rule.
📓 For a deeper dive with additional exercises and analysis, see the complete notebook on GitHub.
🚀 Want to see backpropagation in action? Check out picograd—a minimal automatic differentiation engine I built (inspired by Andrej Karpathy’s micrograd) that implements reverse-mode autodiff from scratch. It demonstrates how computational graphs enable automatic gradient computation through backpropagation!
Training a neural network requires computing gradients of the loss function with respect to every parameter—potentially millions of them. The naive approach of computing each gradient independently would be computationally intractable.
Backpropagation solves this by exploiting the chain rule in a clever way: it reuses intermediate computations to calculate all gradients in a single backward pass through the network. This transforms an exponentially expensive problem into a linear one.
For context on the mathematical foundations of backpropagation, see the Backpropagation summary.
Key Concepts:
Chain Rule in Vector Form: For composite mapping \(z = f(y), y = g(x)\): \[\nabla_x z = \left( \frac{\partial y}{\partial x} \right)^{\top} \nabla_y z\]
Forward Pass: Cache all activations \(h^{(l)} = f^{(l)}(W^{(l)} h^{(l-1)} + b^{(l)})\)
Backward Pass: Propagate gradients layer by layer: \[\nabla_{h^{(l-1)}} L = (W^{(l)})^{\top} (\nabla_{h^{(l)}} L \odot f'^{(l)}(z^{(l)}))\]
Parameter Gradients: \[\frac{\partial L}{\partial W^{(l)}} = (\nabla_{h^{(l)}} L \odot f'^{(l)}(z^{(l)})) (h^{(l-1)})^{\top}\]
| Concept | Description | Key Insight |
|---|---|---|
| Computational Graph | DAG representing operations | Enables reverse-mode automatic differentiation |
| Gradient Reuse | Share intermediate computations | Reduces complexity from exponential to linear |
| Local Gradients | Each operation computes local derivative | Chain rule combines them for global gradient |
How do gradients flow through multiple layers? Let’s trace the chain rule through a 2-layer linear network.
✓ Setup completeLayer 1 (Hidden layer): \[ \begin{align} h_1 &= 2x_1 + x_2 \\ h_2 &= x_1 + 3x_2 \\ h_3 &= -x_1 + x_2 \end{align} \]
Layer 2 (Output layer): \[ \begin{align} y_1 &= h_1 + 2h_2 - h_3 \\ y_2 &= 3h_1 - h_2 + h_3 \end{align} \]
def forward_pass(x: np.ndarray) -> Tuple[np.ndarray, np.ndarray]:
"""
Compute forward pass through the 2-layer network.
Args:
x: Input vector [x1, x2]
Returns:
h: Hidden layer output [h1, h2, h3]
y: Output layer [y1, y2]
"""
x1, x2 = x[0], x[1]
# Layer 1 (linear)
h1 = 2*x1 + x2
h2 = x1 + 3*x2
h3 = -x1 + x2
h = np.array([h1, h2, h3])
# Layer 2 (linear)
y1 = h1 + 2*h2 - h3
y2 = 3*h1 - h2 + h3
y = np.array([y1, y2])
return h, y
print("✓ Forward pass defined")✓ Forward pass definedThe chain rule states: \(\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \frac{\partial \mathbf{y}}{\partial \mathbf{h}} \cdot \frac{\partial \mathbf{h}}{\partial \mathbf{x}}\)
def compute_jacobian_h_x(x: np.ndarray) -> np.ndarray:
"""
Compute ∂h/∂x analytically.
Args:
x: Input vector [x1, x2]
Returns:
Jacobian matrix (3x2)
"""
J = np.array([[2, 1], [1, 3], [-1, 1]])
return J
def compute_jacobian_y_h(x: np.ndarray, h: np.ndarray) -> np.ndarray:
"""
Compute ∂y/∂h analytically.
Args:
x: Input vector [x1, x2]
h: Hidden layer [h1, h2, h3]
Returns:
Jacobian matrix (2x3)
"""
J = np.array([[1, 2, -1], [3, -1, 1]])
return J
def compute_jacobian_y_x(x: np.ndarray) -> np.ndarray:
"""
Compute ∂y/∂x using chain rule.
Args:
x: Input vector [x1, x2]
Returns:
Jacobian matrix (2x2)
"""
return compute_jacobian_y_h(x, forward_pass(x)[0]) @ compute_jacobian_h_x(x)
print("✓ Jacobian functions defined")✓ Jacobian functions defineddef numerical_gradient(func, x, epsilon=1e-7):
"""
Compute numerical gradient using finite differences.
"""
grad = np.zeros((len(func(x)), len(x)))
for i in range(len(x)):
x_plus = x.copy()
x_minus = x.copy()
x_plus[i] += epsilon
x_minus[i] -= epsilon
grad[:, i] = (func(x_plus) - func(x_minus)) / (2 * epsilon)
return grad
# Test at point (1.0, 2.0)
x_test = np.array([1.0, 2.0])
h_test, y_test = forward_pass(x_test)
print(f"Test point: x = {x_test}")
print(f"Hidden layer: h = {h_test}")
print(f"Output: y = {y_test}")
print("\n" + "="*50)
# Compute analytical Jacobians
J_h_x_analytical = compute_jacobian_h_x(x_test)
J_y_h_analytical = compute_jacobian_y_h(x_test, h_test)
J_y_x_analytical = compute_jacobian_y_x(x_test)
# Compute numerical Jacobians
J_h_x_numerical = numerical_gradient(lambda x: forward_pass(x)[0], x_test)
J_y_x_numerical = numerical_gradient(lambda x: forward_pass(x)[1], x_test)
print("\n∂h/∂x (Analytical):")
print(J_h_x_analytical)
print("\n∂h/∂x (Numerical):")
print(J_h_x_numerical)
print(f"\nDifference: {np.max(np.abs(J_h_x_analytical - J_h_x_numerical)):.2e}")
print("\n" + "="*50)
print("\n∂y/∂h (Analytical):")
print(J_y_h_analytical)
print("\n" + "="*50)
print("\n∂y/∂x (Analytical):")
print(J_y_x_analytical)
print("\n∂y/∂x (Numerical):")
print(J_y_x_numerical)
print(f"\nDifference: {np.max(np.abs(J_y_x_analytical - J_y_x_numerical)):.2e}")Test point: x = [1. 2.]
Hidden layer: h = [4. 7. 1.]
Output: y = [17. 6.]
==================================================
∂h/∂x (Analytical):
[[ 2 1]
[ 1 3]
[-1 1]]
∂h/∂x (Numerical):
[[ 2. 1.]
[ 1. 3.]
[-1. 1.]]
Difference: 2.80e-09
==================================================
∂y/∂h (Analytical):
[[ 1 2 -1]
[ 3 -1 1]]
==================================================
∂y/∂x (Analytical):
[[5 6]
[4 1]]
∂y/∂x (Numerical):
[[5.00000002 6. ]
[4. 0.99999999]]
Difference: 2.29e-08Let’s implement a complete 3-layer network with backpropagation and watch how the parameters evolve during training.
Layer 1: \(h^{(1)}_i = \tanh(w^{(1)}_{i1} x_1 + w^{(1)}_{i2} x_2 + b^{(1)}_i)\)
Layer 2: \(h^{(2)}_i = \tanh(w^{(2)}_{i1} a^{(1)}_1 + w^{(2)}_{i2} a^{(1)}_2 + b^{(2)}_i)\)
Output: \(\hat{y} = w^{(3)}_1 a^{(2)}_1 + w^{(3)}_2 a^{(2)}_2 + b^{(3)}\)
Loss: \(L = \frac{1}{2}(\hat{y} - y_{\text{target}})^2\)
class ThreeLayerNetwork:
def __init__(self, seed=42):
"""
Initialize a 3-layer neural network with random weights.
"""
np.random.seed(seed)
# Layer 1: 2 inputs -> 2 hidden units
self.W1 = np.random.randn(2, 2) * 0.5
self.b1 = np.random.randn(2) * 0.5
# Layer 2: 2 hidden -> 2 hidden units
self.W2 = np.random.randn(2, 2) * 0.5
self.b2 = np.random.randn(2) * 0.5
# Layer 3: 2 hidden -> 1 output
self.W3 = np.random.randn(2) * 0.5
self.b3 = np.random.randn() * 0.5
# For storing intermediate values during forward pass
self.cache = {}
def forward(self, x: np.ndarray) -> float:
"""
Forward propagation through the network.
Args:
x: Input vector [x1, x2]
Returns:
y_hat: Predicted output (scalar)
"""
# Store input
self.cache['x'] = x
# Layer 1: h1 = W1 @ x + b1, a1 = tanh(h1)
self.cache['h1'] = self.W1 @ x + self.b1
self.cache['a1'] = np.tanh(self.cache['h1'])
# Layer 2: h2 = W2 @ a1 + b2, a2 = tanh(h2)
self.cache['h2'] = self.W2 @ self.cache['a1'] + self.b2
self.cache['a2'] = np.tanh(self.cache['h2'])
# Layer 3: y_hat = W3 @ a2 + b3 (linear output)
y_hat = self.W3 @ self.cache['a2'] + self.b3
self.cache['y_hat'] = y_hat
return y_hat
def backward(self, y_target: float, learning_rate: float) -> dict:
"""
Backpropagation to compute gradients.
Args:
y_target: Target output (scalar)
learning_rate: Learning rate for gradient descent
Returns:
grads: Dictionary containing gradients for all parameters
"""
# Get cached values
x = self.cache['x']
a1 = self.cache['a1']
a2 = self.cache['a2']
y_hat = self.cache['y_hat']
# Output gradient: dL/dy_hat = y_hat - y_target
dL_dy = y_hat - y_target
# Layer 3 gradients
dL_dW3 = dL_dy * a2 # shape: (2,)
dL_db3 = dL_dy # scalar
dL_da2 = dL_dy * self.W3 # shape: (2,)
# Layer 2 gradients
# tanh derivative: d(tanh(x))/dx = 1 - tanh(x)^2
dL_dh2 = dL_da2 * (1 - a2**2) # shape: (2,)
dL_dW2 = np.outer(dL_dh2, a1) # shape: (2, 2)
dL_db2 = dL_dh2 # shape: (2,)
dL_da1 = self.W2.T @ dL_dh2 # shape: (2,)
# Layer 1 gradients
dL_dh1 = dL_da1 * (1 - a1**2) # shape: (2,)
dL_dW1 = np.outer(dL_dh1, x) # shape: (2, 2)
dL_db1 = dL_dh1 # shape: (2,)
# Store gradients
grads = {
'dW3': dL_dW3,
'db3': dL_db3,
'dW2': dL_dW2,
'db2': dL_db2,
'dW1': dL_dW1,
'db1': dL_db1
}
# Update parameters
self.W3 -= learning_rate * dL_dW3
self.b3 -= learning_rate * dL_db3
self.W2 -= learning_rate * dL_dW2
self.b2 -= learning_rate * dL_db2
self.W1 -= learning_rate * dL_dW1
self.b1 -= learning_rate * dL_db1
return grads
def compute_loss(self, y_hat: float, y_target: float) -> float:
"""
Compute MSE loss.
"""
return 0.5 * (y_hat - y_target)**2
def get_params(self) -> dict:
"""
Get all parameters as a dictionary.
"""
return {
'W1': self.W1.copy(),
'b1': self.b1.copy(),
'W2': self.W2.copy(),
'b2': self.b2.copy(),
'W3': self.W3.copy(),
'b3': self.b3
}
print("✓ Network class defined")✓ Network class defined# Training configuration
x_input = np.array([0.5, -0.3])
y_target = 1.0
learning_rate = 0.01
num_iterations = 1000
# Initialize network
network = ThreeLayerNetwork(seed=42)
# Storage for logging
loss_history = []
param_history = {
'W1': [],
'b1': [],
'W2': [],
'b2': [],
'W3': [],
'b3': []
}
# Training loop
for i in range(num_iterations):
# Forward pass
y_hat = network.forward(x_input)
# Compute loss
loss = network.compute_loss(y_hat, y_target)
loss_history.append(loss)
# Backward pass and parameter update
grads = network.backward(y_target, learning_rate)
# Log parameters
params = network.get_params()
param_history['W1'].append(params['W1'])
param_history['b1'].append(params['b1'])
param_history['W2'].append(params['W2'])
param_history['b2'].append(params['b2'])
param_history['W3'].append(params['W3'])
param_history['b3'].append(params['b3'])
# Print loss every 100 iterations
if (i + 1) % 100 == 0:
print(f"Iteration {i+1:4d}: Loss = {loss:.6f}, y_hat = {y_hat:.6f}")
print("\nTraining completed!")Iteration 100: Loss = 0.019820, y_hat = 0.800902
Iteration 200: Loss = 0.000292, y_hat = 0.975849
Iteration 300: Loss = 0.000004, y_hat = 0.997066
Iteration 400: Loss = 0.000000, y_hat = 0.999644
Iteration 500: Loss = 0.000000, y_hat = 0.999957
Iteration 600: Loss = 0.000000, y_hat = 0.999995
Iteration 700: Loss = 0.000000, y_hat = 0.999999
Iteration 800: Loss = 0.000000, y_hat = 1.000000
Iteration 900: Loss = 0.000000, y_hat = 1.000000
Iteration 1000: Loss = 0.000000, y_hat = 1.000000
Training completed!plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(loss_history)
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Training Loss over Time')
plt.grid(True)
plt.yscale('log')
plt.subplot(1, 2, 2)
plt.plot(loss_history[-500:])
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Loss (Last 500 iterations)')
plt.grid(True)
plt.tight_layout()
plt.show()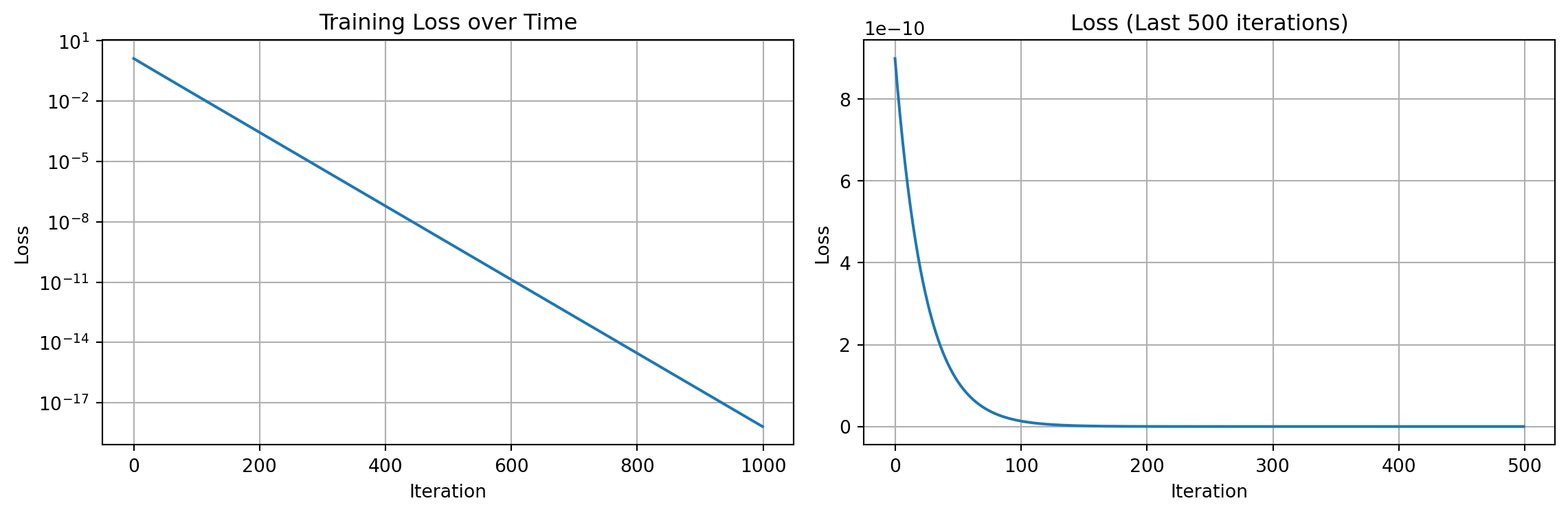
fig, axes = plt.subplots(2, 3, figsize=(15, 8))
# W1
axes[0, 0].plot(np.array(param_history['W1'])[:, 0, 0], label='W1[0,0]')
axes[0, 0].plot(np.array(param_history['W1'])[:, 0, 1], label='W1[0,1]')
axes[0, 0].plot(np.array(param_history['W1'])[:, 1, 0], label='W1[1,0]')
axes[0, 0].plot(np.array(param_history['W1'])[:, 1, 1], label='W1[1,1]')
axes[0, 0].set_title('Layer 1 Weights (W1)')
axes[0, 0].legend()
axes[0, 0].grid(True)
# b1
axes[0, 1].plot(np.array(param_history['b1'])[:, 0], label='b1[0]')
axes[0, 1].plot(np.array(param_history['b1'])[:, 1], label='b1[1]')
axes[0, 1].set_title('Layer 1 Biases (b1)')
axes[0, 1].legend()
axes[0, 1].grid(True)
# W2
axes[0, 2].plot(np.array(param_history['W2'])[:, 0, 0], label='W2[0,0]')
axes[0, 2].plot(np.array(param_history['W2'])[:, 0, 1], label='W2[0,1]')
axes[0, 2].plot(np.array(param_history['W2'])[:, 1, 0], label='W2[1,0]')
axes[0, 2].plot(np.array(param_history['W2'])[:, 1, 1], label='W2[1,1]')
axes[0, 2].set_title('Layer 2 Weights (W2)')
axes[0, 2].legend()
axes[0, 2].grid(True)
# b2
axes[1, 0].plot(np.array(param_history['b2'])[:, 0], label='b2[0]')
axes[1, 0].plot(np.array(param_history['b2'])[:, 1], label='b2[1]')
axes[1, 0].set_title('Layer 2 Biases (b2)')
axes[1, 0].legend()
axes[1, 0].grid(True)
# W3
axes[1, 1].plot(np.array(param_history['W3'])[:, 0], label='W3[0]')
axes[1, 1].plot(np.array(param_history['W3'])[:, 1], label='W3[1]')
axes[1, 1].set_title('Layer 3 Weights (W3)')
axes[1, 1].legend()
axes[1, 1].grid(True)
# b3
axes[1, 2].plot(param_history['b3'], label='b3')
axes[1, 2].set_title('Layer 3 Bias (b3)')
axes[1, 2].legend()
axes[1, 2].grid(True)
for ax in axes.flat:
ax.set_xlabel('Iteration')
ax.set_ylabel('Parameter Value')
plt.tight_layout()
plt.show()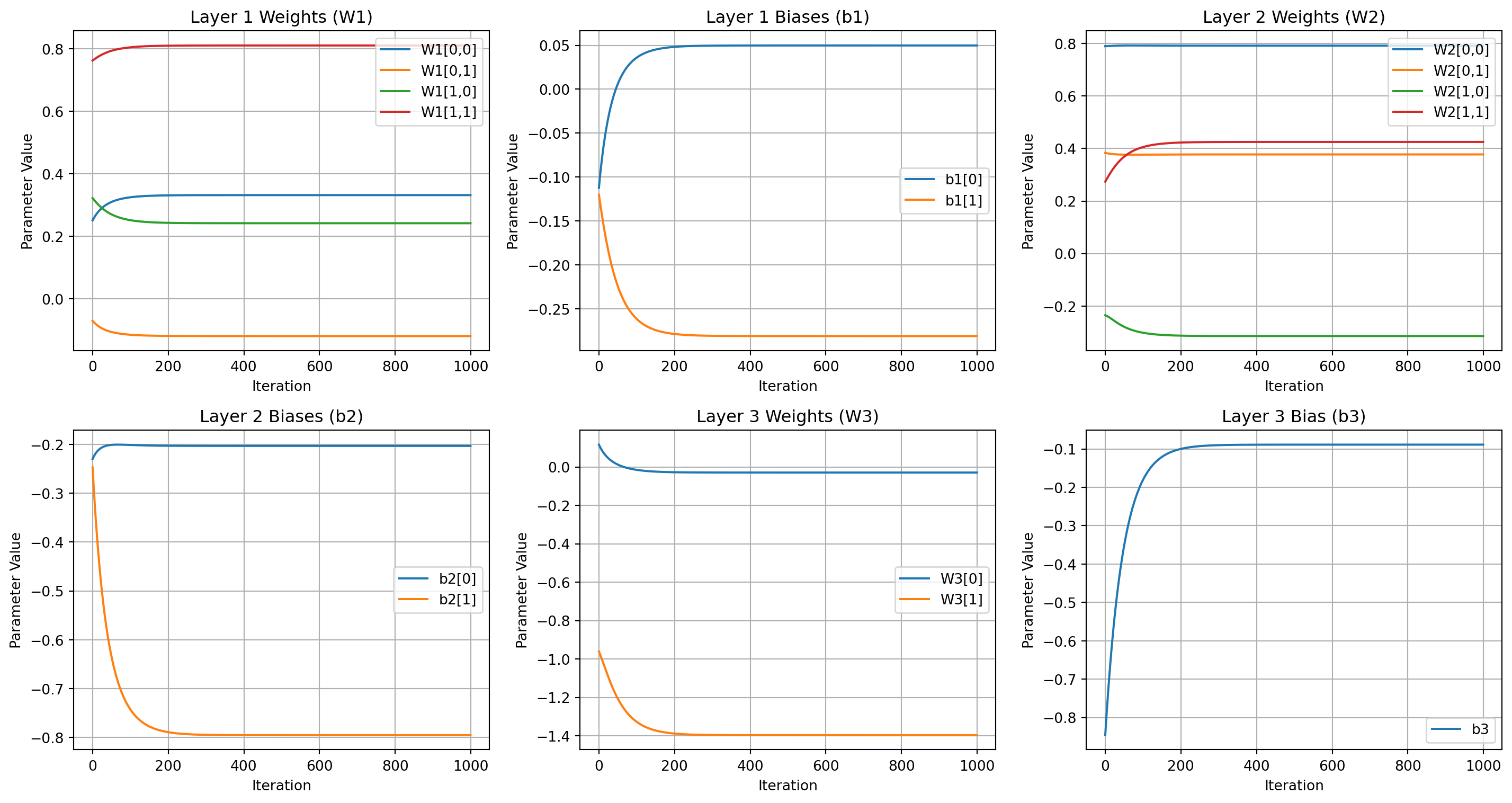
print("\n" + "="*60)
print("TRAINING SUMMARY")
print("="*60)
print(f"Initial Loss: {loss_history[0]:.6f}")
print(f"Final Loss: {loss_history[-1]:.6f}")
print(f"Loss Reduction: {(1 - loss_history[-1]/loss_history[0])*100:.2f}%")
print(f"\nTarget: {y_target}")
final_prediction = network.forward(x_input)
print(f"Final Prediction: {final_prediction:.6f}")
print(f"Prediction Error: {abs(final_prediction - y_target):.6f}")
============================================================
TRAINING SUMMARY
============================================================
Initial Loss: 1.323064
Final Loss: 0.000000
Loss Reduction: 100.00%
Target: 1.0
Final Prediction: 1.000000
Prediction Error: 0.000000This implementation demonstrates the power of backpropagation: efficiently computing gradients through the chain rule enables training deep neural networks that would otherwise be computationally intractable.
---
title: "Goodfellow Deep Learning — Deep Learning Book 6.5: Back-Propagation and Other Differentiation Algorithms"
author: "Chao Ma"
date: "2025-10-02"
categories: ["Deep Learning", "Backpropagation", "Neural Networks"]
code-fold: true
code-summary: "Show code"
---
*This recap of Deep Learning Chapter 6.5 explores backpropagation—the algorithm that makes training deep neural networks computationally feasible by efficiently computing gradients through the chain rule.*
📓 **For a deeper dive with additional exercises and analysis**, see the [complete notebook on GitHub](https://github.com/ickma2311/foundations/blob/main/deep_learning/chapter6/6.5/exercises.ipynb).
🚀 **Want to see backpropagation in action?** Check out [**picograd**](https://github.com/ickma2311/picograd)—a minimal automatic differentiation engine I built (inspired by Andrej Karpathy's micrograd) that implements reverse-mode autodiff from scratch. It demonstrates how computational graphs enable automatic gradient computation through backpropagation!
## The Gradient Problem: Why Backpropagation?
Training a neural network requires computing gradients of the loss function with respect to every parameter—potentially millions of them. The naive approach of computing each gradient independently would be computationally intractable.
**Backpropagation** solves this by exploiting the chain rule in a clever way: it reuses intermediate computations to calculate all gradients in a single backward pass through the network. This transforms an exponentially expensive problem into a linear one.
### Quick Reference: Understanding Backpropagation
For context on the mathematical foundations of backpropagation, see the [Backpropagation summary](https://github.com/ickma2311/foundations/blob/main/deep_learning/chapter6/6.5/backpropagation_summary.md).
**Key Concepts**:
1. **Chain Rule in Vector Form**: For composite mapping $z = f(y), y = g(x)$:
$$\nabla_x z = \left( \frac{\partial y}{\partial x} \right)^{\top} \nabla_y z$$
2. **Forward Pass**: Cache all activations $h^{(l)} = f^{(l)}(W^{(l)} h^{(l-1)} + b^{(l)})$
3. **Backward Pass**: Propagate gradients layer by layer:
$$\nabla_{h^{(l-1)}} L = (W^{(l)})^{\top} (\nabla_{h^{(l)}} L \odot f'^{(l)}(z^{(l)}))$$
4. **Parameter Gradients**:
$$\frac{\partial L}{\partial W^{(l)}} = (\nabla_{h^{(l)}} L \odot f'^{(l)}(z^{(l)})) (h^{(l-1)})^{\top}$$
| **Concept** | **Description** | **Key Insight** |
|-------------|-----------------|-----------------|
| **Computational Graph** | DAG representing operations | Enables reverse-mode automatic differentiation |
| **Gradient Reuse** | Share intermediate computations | Reduces complexity from exponential to linear |
| **Local Gradients** | Each operation computes local derivative | Chain rule combines them for global gradient |
## 🔬 Exercise 1: Understanding Jacobian Matrices
How do gradients flow through multiple layers? Let's trace the chain rule through a 2-layer linear network.
```{python}
import numpy as np
import matplotlib.pyplot as plt
from typing import Tuple
# Set random seed for reproducibility
np.random.seed(42)
print("✓ Setup complete")
```
### The 2-Layer Network
**Layer 1 (Hidden layer):**
$$
\begin{align}
h_1 &= 2x_1 + x_2 \\
h_2 &= x_1 + 3x_2 \\
h_3 &= -x_1 + x_2
\end{align}
$$
**Layer 2 (Output layer):**
$$
\begin{align}
y_1 &= h_1 + 2h_2 - h_3 \\
y_2 &= 3h_1 - h_2 + h_3
\end{align}
$$
### Forward Pass Implementation
```{python}
def forward_pass(x: np.ndarray) -> Tuple[np.ndarray, np.ndarray]:
"""
Compute forward pass through the 2-layer network.
Args:
x: Input vector [x1, x2]
Returns:
h: Hidden layer output [h1, h2, h3]
y: Output layer [y1, y2]
"""
x1, x2 = x[0], x[1]
# Layer 1 (linear)
h1 = 2*x1 + x2
h2 = x1 + 3*x2
h3 = -x1 + x2
h = np.array([h1, h2, h3])
# Layer 2 (linear)
y1 = h1 + 2*h2 - h3
y2 = 3*h1 - h2 + h3
y = np.array([y1, y2])
return h, y
print("✓ Forward pass defined")
```
### Computing Jacobian Matrices
The chain rule states: $\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \frac{\partial \mathbf{y}}{\partial \mathbf{h}} \cdot \frac{\partial \mathbf{h}}{\partial \mathbf{x}}$
```{python}
def compute_jacobian_h_x(x: np.ndarray) -> np.ndarray:
"""
Compute ∂h/∂x analytically.
Args:
x: Input vector [x1, x2]
Returns:
Jacobian matrix (3x2)
"""
J = np.array([[2, 1], [1, 3], [-1, 1]])
return J
def compute_jacobian_y_h(x: np.ndarray, h: np.ndarray) -> np.ndarray:
"""
Compute ∂y/∂h analytically.
Args:
x: Input vector [x1, x2]
h: Hidden layer [h1, h2, h3]
Returns:
Jacobian matrix (2x3)
"""
J = np.array([[1, 2, -1], [3, -1, 1]])
return J
def compute_jacobian_y_x(x: np.ndarray) -> np.ndarray:
"""
Compute ∂y/∂x using chain rule.
Args:
x: Input vector [x1, x2]
Returns:
Jacobian matrix (2x2)
"""
return compute_jacobian_y_h(x, forward_pass(x)[0]) @ compute_jacobian_h_x(x)
print("✓ Jacobian functions defined")
```
### Verification with Numerical Gradients
```{python}
def numerical_gradient(func, x, epsilon=1e-7):
"""
Compute numerical gradient using finite differences.
"""
grad = np.zeros((len(func(x)), len(x)))
for i in range(len(x)):
x_plus = x.copy()
x_minus = x.copy()
x_plus[i] += epsilon
x_minus[i] -= epsilon
grad[:, i] = (func(x_plus) - func(x_minus)) / (2 * epsilon)
return grad
# Test at point (1.0, 2.0)
x_test = np.array([1.0, 2.0])
h_test, y_test = forward_pass(x_test)
print(f"Test point: x = {x_test}")
print(f"Hidden layer: h = {h_test}")
print(f"Output: y = {y_test}")
print("\n" + "="*50)
# Compute analytical Jacobians
J_h_x_analytical = compute_jacobian_h_x(x_test)
J_y_h_analytical = compute_jacobian_y_h(x_test, h_test)
J_y_x_analytical = compute_jacobian_y_x(x_test)
# Compute numerical Jacobians
J_h_x_numerical = numerical_gradient(lambda x: forward_pass(x)[0], x_test)
J_y_x_numerical = numerical_gradient(lambda x: forward_pass(x)[1], x_test)
print("\n∂h/∂x (Analytical):")
print(J_h_x_analytical)
print("\n∂h/∂x (Numerical):")
print(J_h_x_numerical)
print(f"\nDifference: {np.max(np.abs(J_h_x_analytical - J_h_x_numerical)):.2e}")
print("\n" + "="*50)
print("\n∂y/∂h (Analytical):")
print(J_y_h_analytical)
print("\n" + "="*50)
print("\n∂y/∂x (Analytical):")
print(J_y_x_analytical)
print("\n∂y/∂x (Numerical):")
print(J_y_x_numerical)
print(f"\nDifference: {np.max(np.abs(J_y_x_analytical - J_y_x_numerical)):.2e}")
```
## 🔬 Exercise 2: Gradient Descent with Backpropagation
Let's implement a complete 3-layer network with backpropagation and watch how the parameters evolve during training.
### Network Architecture
**Layer 1:** $h^{(1)}_i = \tanh(w^{(1)}_{i1} x_1 + w^{(1)}_{i2} x_2 + b^{(1)}_i)$
**Layer 2:** $h^{(2)}_i = \tanh(w^{(2)}_{i1} a^{(1)}_1 + w^{(2)}_{i2} a^{(1)}_2 + b^{(2)}_i)$
**Output:** $\hat{y} = w^{(3)}_1 a^{(2)}_1 + w^{(3)}_2 a^{(2)}_2 + b^{(3)}$
**Loss:** $L = \frac{1}{2}(\hat{y} - y_{\text{target}})^2$
### Implementation
```{python}
class ThreeLayerNetwork:
def __init__(self, seed=42):
"""
Initialize a 3-layer neural network with random weights.
"""
np.random.seed(seed)
# Layer 1: 2 inputs -> 2 hidden units
self.W1 = np.random.randn(2, 2) * 0.5
self.b1 = np.random.randn(2) * 0.5
# Layer 2: 2 hidden -> 2 hidden units
self.W2 = np.random.randn(2, 2) * 0.5
self.b2 = np.random.randn(2) * 0.5
# Layer 3: 2 hidden -> 1 output
self.W3 = np.random.randn(2) * 0.5
self.b3 = np.random.randn() * 0.5
# For storing intermediate values during forward pass
self.cache = {}
def forward(self, x: np.ndarray) -> float:
"""
Forward propagation through the network.
Args:
x: Input vector [x1, x2]
Returns:
y_hat: Predicted output (scalar)
"""
# Store input
self.cache['x'] = x
# Layer 1: h1 = W1 @ x + b1, a1 = tanh(h1)
self.cache['h1'] = self.W1 @ x + self.b1
self.cache['a1'] = np.tanh(self.cache['h1'])
# Layer 2: h2 = W2 @ a1 + b2, a2 = tanh(h2)
self.cache['h2'] = self.W2 @ self.cache['a1'] + self.b2
self.cache['a2'] = np.tanh(self.cache['h2'])
# Layer 3: y_hat = W3 @ a2 + b3 (linear output)
y_hat = self.W3 @ self.cache['a2'] + self.b3
self.cache['y_hat'] = y_hat
return y_hat
def backward(self, y_target: float, learning_rate: float) -> dict:
"""
Backpropagation to compute gradients.
Args:
y_target: Target output (scalar)
learning_rate: Learning rate for gradient descent
Returns:
grads: Dictionary containing gradients for all parameters
"""
# Get cached values
x = self.cache['x']
a1 = self.cache['a1']
a2 = self.cache['a2']
y_hat = self.cache['y_hat']
# Output gradient: dL/dy_hat = y_hat - y_target
dL_dy = y_hat - y_target
# Layer 3 gradients
dL_dW3 = dL_dy * a2 # shape: (2,)
dL_db3 = dL_dy # scalar
dL_da2 = dL_dy * self.W3 # shape: (2,)
# Layer 2 gradients
# tanh derivative: d(tanh(x))/dx = 1 - tanh(x)^2
dL_dh2 = dL_da2 * (1 - a2**2) # shape: (2,)
dL_dW2 = np.outer(dL_dh2, a1) # shape: (2, 2)
dL_db2 = dL_dh2 # shape: (2,)
dL_da1 = self.W2.T @ dL_dh2 # shape: (2,)
# Layer 1 gradients
dL_dh1 = dL_da1 * (1 - a1**2) # shape: (2,)
dL_dW1 = np.outer(dL_dh1, x) # shape: (2, 2)
dL_db1 = dL_dh1 # shape: (2,)
# Store gradients
grads = {
'dW3': dL_dW3,
'db3': dL_db3,
'dW2': dL_dW2,
'db2': dL_db2,
'dW1': dL_dW1,
'db1': dL_db1
}
# Update parameters
self.W3 -= learning_rate * dL_dW3
self.b3 -= learning_rate * dL_db3
self.W2 -= learning_rate * dL_dW2
self.b2 -= learning_rate * dL_db2
self.W1 -= learning_rate * dL_dW1
self.b1 -= learning_rate * dL_db1
return grads
def compute_loss(self, y_hat: float, y_target: float) -> float:
"""
Compute MSE loss.
"""
return 0.5 * (y_hat - y_target)**2
def get_params(self) -> dict:
"""
Get all parameters as a dictionary.
"""
return {
'W1': self.W1.copy(),
'b1': self.b1.copy(),
'W2': self.W2.copy(),
'b2': self.b2.copy(),
'W3': self.W3.copy(),
'b3': self.b3
}
print("✓ Network class defined")
```
### Training Loop
```{python}
# Training configuration
x_input = np.array([0.5, -0.3])
y_target = 1.0
learning_rate = 0.01
num_iterations = 1000
# Initialize network
network = ThreeLayerNetwork(seed=42)
# Storage for logging
loss_history = []
param_history = {
'W1': [],
'b1': [],
'W2': [],
'b2': [],
'W3': [],
'b3': []
}
# Training loop
for i in range(num_iterations):
# Forward pass
y_hat = network.forward(x_input)
# Compute loss
loss = network.compute_loss(y_hat, y_target)
loss_history.append(loss)
# Backward pass and parameter update
grads = network.backward(y_target, learning_rate)
# Log parameters
params = network.get_params()
param_history['W1'].append(params['W1'])
param_history['b1'].append(params['b1'])
param_history['W2'].append(params['W2'])
param_history['b2'].append(params['b2'])
param_history['W3'].append(params['W3'])
param_history['b3'].append(params['b3'])
# Print loss every 100 iterations
if (i + 1) % 100 == 0:
print(f"Iteration {i+1:4d}: Loss = {loss:.6f}, y_hat = {y_hat:.6f}")
print("\nTraining completed!")
```
### Visualization: Loss Curve
```{python}
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(loss_history)
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Training Loss over Time')
plt.grid(True)
plt.yscale('log')
plt.subplot(1, 2, 2)
plt.plot(loss_history[-500:])
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Loss (Last 500 iterations)')
plt.grid(True)
plt.tight_layout()
plt.show()
```
### Visualization: Parameter Evolution
```{python}
fig, axes = plt.subplots(2, 3, figsize=(15, 8))
# W1
axes[0, 0].plot(np.array(param_history['W1'])[:, 0, 0], label='W1[0,0]')
axes[0, 0].plot(np.array(param_history['W1'])[:, 0, 1], label='W1[0,1]')
axes[0, 0].plot(np.array(param_history['W1'])[:, 1, 0], label='W1[1,0]')
axes[0, 0].plot(np.array(param_history['W1'])[:, 1, 1], label='W1[1,1]')
axes[0, 0].set_title('Layer 1 Weights (W1)')
axes[0, 0].legend()
axes[0, 0].grid(True)
# b1
axes[0, 1].plot(np.array(param_history['b1'])[:, 0], label='b1[0]')
axes[0, 1].plot(np.array(param_history['b1'])[:, 1], label='b1[1]')
axes[0, 1].set_title('Layer 1 Biases (b1)')
axes[0, 1].legend()
axes[0, 1].grid(True)
# W2
axes[0, 2].plot(np.array(param_history['W2'])[:, 0, 0], label='W2[0,0]')
axes[0, 2].plot(np.array(param_history['W2'])[:, 0, 1], label='W2[0,1]')
axes[0, 2].plot(np.array(param_history['W2'])[:, 1, 0], label='W2[1,0]')
axes[0, 2].plot(np.array(param_history['W2'])[:, 1, 1], label='W2[1,1]')
axes[0, 2].set_title('Layer 2 Weights (W2)')
axes[0, 2].legend()
axes[0, 2].grid(True)
# b2
axes[1, 0].plot(np.array(param_history['b2'])[:, 0], label='b2[0]')
axes[1, 0].plot(np.array(param_history['b2'])[:, 1], label='b2[1]')
axes[1, 0].set_title('Layer 2 Biases (b2)')
axes[1, 0].legend()
axes[1, 0].grid(True)
# W3
axes[1, 1].plot(np.array(param_history['W3'])[:, 0], label='W3[0]')
axes[1, 1].plot(np.array(param_history['W3'])[:, 1], label='W3[1]')
axes[1, 1].set_title('Layer 3 Weights (W3)')
axes[1, 1].legend()
axes[1, 1].grid(True)
# b3
axes[1, 2].plot(param_history['b3'], label='b3')
axes[1, 2].set_title('Layer 3 Bias (b3)')
axes[1, 2].legend()
axes[1, 2].grid(True)
for ax in axes.flat:
ax.set_xlabel('Iteration')
ax.set_ylabel('Parameter Value')
plt.tight_layout()
plt.show()
```
### Final Results
```{python}
print("\n" + "="*60)
print("TRAINING SUMMARY")
print("="*60)
print(f"Initial Loss: {loss_history[0]:.6f}")
print(f"Final Loss: {loss_history[-1]:.6f}")
print(f"Loss Reduction: {(1 - loss_history[-1]/loss_history[0])*100:.2f}%")
print(f"\nTarget: {y_target}")
final_prediction = network.forward(x_input)
print(f"Final Prediction: {final_prediction:.6f}")
print(f"Prediction Error: {abs(final_prediction - y_target):.6f}")
```
---
*This implementation demonstrates the power of backpropagation: efficiently computing gradients through the chain rule enables training deep neural networks that would otherwise be computationally intractable.*