Lecture 12: Graphs, Networks, and Incidence Matrices
Overview
This lecture connects linear algebra to graph theory and electrical networks:
- Incidence matrices: Representing graphs with matrices
- Four fundamental subspaces: Applied to graphs (loops and potential differences)
- Ohm’s law: Relating currents to potential differences
- Kirchhoff’s laws: Current conservation and voltage laws
- Euler’s formula: Relationship between nodes, edges, and loops
1. Graph Representation with Incidence Matrix
Example Graph
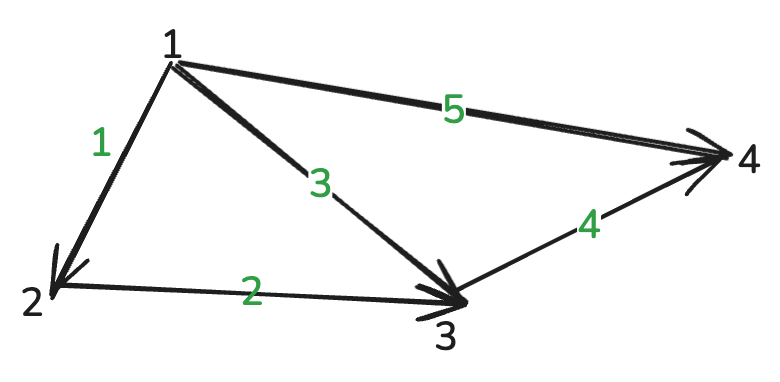
Graph structure:
- 4 nodes (vertices)
- 5 edges
Incidence Matrix
\[ A = \begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ 0 & 0 & -1 & 1 \\ -1 & 0 & 0 & 1 \end{bmatrix} \]
Dimensions: \(A\) is \(5 \times 4\) (m × n matrix)
- \(m = 5\): number of edges (rows)
- \(n = 4\): number of nodes (columns)
Structure:
- Each row represents an edge
- Each edge has exactly one \(-1\) (starting node) and one \(+1\) (ending node)
- The rest are zeros
Example: First row \([-1, 1, 0, 0]\) represents an edge from node 1 to node 2.
2. Null Space of \(A\): Constant Potentials
Finding \(N(A)\)
To find \(N(A)\), we solve \(Ax = \mathbf{0}\):
\[ \begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ 0 & 0 & -1 & 1 \\ -1 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} \]
This gives us the system:
- Row 1: \(-x_1 + x_2 = 0\) → \(x_1 = x_2\)
- Row 2: \(-x_2 + x_3 = 0\) → \(x_2 = x_3\)
- Row 4: \(-x_3 + x_4 = 0\) → \(x_3 = x_4\)
From these equations: \(x_1 = x_2 = x_3 = x_4\)
Solution: \[ N(A) = c \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \]
Dimension: \(\dim(N(A)) = 1\)
Interpretation:
- The null space represents constant potentials across all nodes
- If all nodes have the same potential, there is no voltage difference across any edge
- This corresponds to setting all nodes to the same “ground level”
Rank calculation: \[ \text{rank}(A) = n - \dim(N(A)) = 4 - 1 = 3 \]
3. Left Null Space of \(A\): Loops
Transpose Matrix
\[ A^T = \begin{bmatrix} -1 & 0 & -1 & 0 & -1 \\ 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & 1 & -1 & 0 \\ 0 & 0 & 0 & 1 & 1 \end{bmatrix} \]
Dimensions: \(4 \times 5\) (n × m matrix)
Structure:
- Each column represents an edge
- Each row represents a node
- Row \(i\) shows: which edges flow out of node \(i\) (-1) and which flow in (+1)
Node balance:
- Node 1: 3 edges out (edges 1, 3, 5)
- Node 2: 1 edge in (edge 1), 1 edge out (edge 2)
- Node 3: 2 edges in (edges 2, 3), 1 edge out (edge 4)
- Node 4: 2 edges in (edges 4, 5)
Key property: Each column sums to \(-1 + 1 = 0\).
Finding \(N(A^T)\)
Dimension:
\[ \dim(N(A^T)) = m - r = 5 - 3 = 2 \]
System of equations: \(A^T y = \mathbf{0}\) gives:
\[ \begin{aligned} y_1 + y_3 + y_5 &= 0 \\ y_1 - y_2 &= 0 \\ y_2 + y_3 - y_4 &= 0 \\ y_4 + y_5 &= 0 \end{aligned} \]
Solution process:
- Set \(y_1 = 1\), then \(y_2 = 1\) (from equation 2)
- Set \(y_3 = -1\) to satisfy equation 1 (with \(y_5 = 0\))
- This gives the first loop: edges 1, 2, 3
For the second loop:
- Set \(y_4 = 1\), then \(y_5 = -1\) (from equation 4)
- Set \(y_1 = y_2 = y_3 = 0\)
- This gives the second loop: edges 4, 5
Basis for \(N(A^T)\):
\[ N(A^T) = c_1 \begin{bmatrix} 1 \\ 1 \\ -1 \\ 0 \\ 0 \end{bmatrix} + c_2 \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ -1 \end{bmatrix} \]
Interpretation:
- Loop 1: edges 1 → 2 → 3 form a cycle
- Loop 2: edges 4 → 5 form a cycle
- The \(-1\) entries indicate edges traversed in the opposite direction
4. Currents and Potentials
Definitions
Potential (\(u_i\)):
- Associated with nodes
- Represents “voltage” or “energy level” at each node
Current (\(x_i\)):
- Associated with edges
- Represents flow of charge or material along edges
5. Ohm’s Law
Statement: The current on an edge is proportional to the potential drop across that edge.
Mathematical form:
\[ x_{ij} = u_i - u_j \]
where:
- \(x_{ij}\): current on edge from node \(i\) to node \(j\)
- \(u_i\), \(u_j\): potentials at nodes \(i\) and \(j\)
Matrix form:
\[ x = A u \]
Interpretation:
- \(Au\) maps node potentials to edge currents
- Each current is the difference in potential between the edge’s endpoints
6. Kirchhoff’s Current Law
Statement: The total current flowing into a node equals the total current flowing out.
Mathematical form:
\[ A^T y = \mathbf{0} \]
where \(y\) is the vector of edge currents.
Physical interpretation: “In equals out” — charge conservation at each node.
Connection to left null space: Kirchhoff’s current law defines exactly the left null space of \(A\), which represents the valid current patterns (loops) in the graph.
7. Graph Properties
Tree
Definition: A graph without loops.
Properties:
- A tree on \(n\) nodes has exactly \(n - 1\) edges
- \(\text{rank}(A) = n - 1\) for a tree
- \(\dim(N(A^T)) = 0\) (no loops)
Loops
Number of loops:
\[ \text{number of loops} = \dim(N(A^T)) = m - r \]
where:
- \(m\) = number of edges
- \(r\) = rank of \(A\) = (number of nodes - 1)
For our example:
- Number of loops = \(5 - 3 = 2\)
8. Euler’s Formula
Formula:
\[ (\text{nodes}) - (\text{edges}) + (\text{loops}) = 1 \]
Derivation using rank-nullity:
\[ \begin{aligned} \text{loops} &= m - r \\ &= m - (n - 1) \\ &= m - n + 1 \end{aligned} \]
Rearranging:
\[ n - m + (\text{loops}) = 1 \]
For our example:
\[ 4 - 5 + 2 = 1 \quad \checkmark \]
Interpretation: This fundamental relationship connects graph topology to linear algebra through the rank-nullity theorem.
Key concepts:
- Incidence matrix \(A\): Rows = edges, columns = nodes; entries are \(-1\), \(0\), \(+1\)
- \(N(A)\): Constant potentials (dimension = 1)
- \(N(A^T)\): Loops in the graph (dimension = number of loops)
- Rank: \(\text{rank}(A) = n - 1\) (number of nodes - 1)
- Ohm’s law: \(x = A^T u\) (currents from potentials)
- Kirchhoff’s law: \(A^T y = \mathbf{0}\) (current conservation)
- Euler’s formula: (nodes) - (edges) + (loops) = 1
Physical applications:
- Electrical networks and circuits
- Flow networks and transportation
- Communication networks
- Structural engineering (trusses)
Source: MIT 18.06SC Linear Algebra, Lecture 12