Deep Learning Book 6.4: Architecture Design - Depth vs Width

Deep Learning
Neural Networks
Architecture Design
Author

Chao Ma

Published

September 30, 2025

This recap of Deep Learning Chapter 6.4 explores how network architecture—depth versus width—fundamentally shapes what neural networks can learn and how efficiently they learn it.

📓 For a deeper dive with additional exercises and analysis, see the complete notebook on GitHub.

The Architecture Question: Deep or Wide?

When designing a neural network, one of the most fundamental decisions is choosing between depth (many layers) and width (many units per layer). Should you build a shallow network with many units, or a deep network with fewer units per layer?

The answer reveals something profound about how neural networks represent functions: deep networks can achieve exponentially greater expressiveness than shallow networks with the same number of parameters. This isn’t just theoretical—it has practical implications for model efficiency and performance.

Quick Reference: Understanding Depth vs Width

For context on the fundamental concepts of network architecture, see the Architecture Design summary.

Key insight: A deep ReLU network with \(n\) units per layer and depth \(L\) can create \(\mathcal{O}(n^L)\) distinct linear regions in the input space. A shallow network would need exponentially many units (\(\mathcal{O}(n^L)\) units in a single layer) to achieve the same expressiveness.

Architecture Characteristic Advantage Challenge
Deep (many layers) Hierarchical feature reuse Exponential expressiveness with fewer parameters Harder to optimize (vanishing/exploding gradients)
Wide (many units per layer) Increased capacity per layer Easier optimization Parameter inefficient; requires exponentially more units

🔬 Experiment: Shallow vs Deep Network Comparison

Let’s explore whether depth provides an advantage in practice by comparing two networks: - Shallow Network: 1 hidden layer with 128 units - Deep Network: 3 hidden layers (16 → 8 → output)

Both networks are trained on the same regression task: \(y = \sin^2(x) + x^3\)

Show code 
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn

# Set random seed for reproducibility
np.random.seed(42)
torch.manual_seed(42)

# Configure plotting
plt.rcParams['figure.facecolor'] = 'white'
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['axes.grid'] = True
plt.rcParams['grid.alpha'] = 0.3

print("✓ Setup complete")
✓ Setup complete

Step 1: Generate Training and Test Data

Show code 
# Training data
x_train = np.random.rand(200, 1)
y_train = np.square(np.sin(x_train)) + np.power(x_train, 3)

# Test data
x_test = np.random.rand(100, 1)
y_test = np.square(np.sin(x_test)) + np.power(x_test, 3)

# Convert to PyTorch tensors
x_train_tensor = torch.FloatTensor(x_train)
y_train_tensor = torch.FloatTensor(y_train)
x_test_tensor = torch.FloatTensor(x_test)
y_test_tensor = torch.FloatTensor(y_test)

print(f"Training samples: {len(x_train)}")
print(f"Test samples: {len(x_test)}")
print(f"Input range: [{x_train.min():.2f}, {x_train.max():.2f}]")
print(f"Target range: [{y_train.min():.2f}, {y_train.max():.2f}]")
Training samples: 200
Test samples: 100
Input range: [0.01, 0.99]
Target range: [0.00, 1.66]

Step 2: Define Model Architectures

Show code 
# Shallow model: 1 hidden layer with 128 units
shallow_model = nn.Sequential(
    nn.Linear(1, 128),
    nn.ReLU(),
    nn.Linear(128, 1)
)

# Deep model: 3 hidden layers (16 → 8 → output)
deep_model = nn.Sequential(
    nn.Linear(1, 16),
    nn.ReLU(),
    nn.Linear(16, 8),
    nn.ReLU(),
    nn.Linear(8, 1)
)

print("✓ Models created")
print(f"\nShallow model architecture:")
print(shallow_model)
print(f"\nDeep model architecture:")
print(deep_model)
✓ Models created

Shallow model architecture:
Sequential(
  (0): Linear(in_features=1, out_features=128, bias=True)
  (1): ReLU()
  (2): Linear(in_features=128, out_features=1, bias=True)
)

Deep model architecture:
Sequential(
  (0): Linear(in_features=1, out_features=16, bias=True)
  (1): ReLU()
  (2): Linear(in_features=16, out_features=8, bias=True)
  (3): ReLU()
  (4): Linear(in_features=8, out_features=1, bias=True)
)

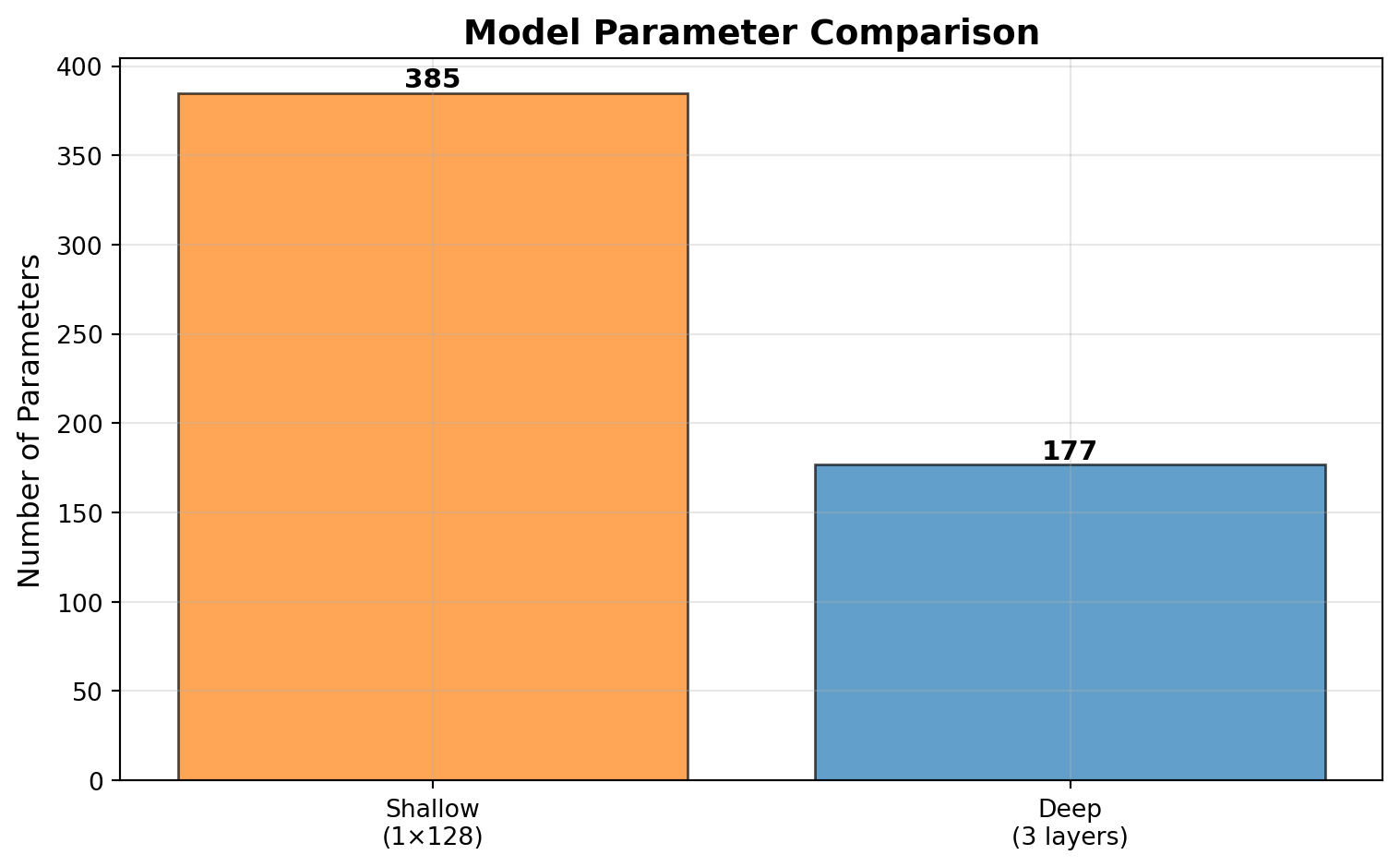
Step 3: Count Parameters

How many trainable parameters does each architecture use?

Show code 
def count_parameters(model):
    """Count total trainable parameters in a model"""
    return sum(p.numel() for p in model.parameters() if p.requires_grad)

shallow_params = count_parameters(shallow_model)
deep_params = count_parameters(deep_model)

print("Parameter Counts:")
print("-" * 50)
print(f"Shallow model (1 layer × 128 units): {shallow_params:,} parameters")
print(f"Deep model (3 layers):                {deep_params:,} parameters")
print("-" * 50)
print(f"Ratio (shallow/deep): {shallow_params/deep_params:.2f}x")

# Visualize parameter counts
fig, ax = plt.subplots(figsize=(8, 5))
models = ['Shallow\n(1×128)', 'Deep\n(3 layers)']
params = [shallow_params, deep_params]
colors = ['#ff7f0e', '#1f77b4']

bars = ax.bar(models, params, color=colors, alpha=0.7, edgecolor='black')
ax.set_ylabel('Number of Parameters', fontsize=12)
ax.set_title('Model Parameter Comparison', fontsize=14, fontweight='bold')
ax.grid(axis='y', alpha=0.3)

# Add value labels on bars
for bar, param in zip(bars, params):
    height = bar.get_height()
    ax.text(bar.get_x() + bar.get_width()/2., height,
            f'{param:,}',
            ha='center', va='bottom', fontsize=11, fontweight='bold')

plt.tight_layout()
plt.show()
Parameter Counts:
--------------------------------------------------
Shallow model (1 layer × 128 units): 385 parameters
Deep model (3 layers):                177 parameters
--------------------------------------------------
Ratio (shallow/deep): 2.18x

Step 4: Train Both Models

Show code 
# Training configuration
n_epochs = 500
learning_rate = 0.01
loss_fn = nn.MSELoss()

# Track training history
history = {
    'Shallow': {'train_loss': [], 'test_loss': []},
    'Deep': {'train_loss': [], 'test_loss': []}
}

models = {
    'Shallow': shallow_model,
    'Deep': deep_model
}

# Train each model
for name, model in models.items():
    optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

    for epoch in range(n_epochs):
        # Training
        model.train()
        y_pred = model(x_train_tensor)
        loss = loss_fn(y_pred, y_train_tensor)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        history[name]['train_loss'].append(loss.item())

        # Evaluation on test set
        model.eval()
        with torch.no_grad():
            y_test_pred = model(x_test_tensor)
            test_loss = loss_fn(y_test_pred, y_test_tensor).item()
            history[name]['test_loss'].append(test_loss)

    print(f"✓ {name} model trained")

print("\n✓ Training complete")
✓ Shallow model trained
✓ Deep model trained

✓ Training complete

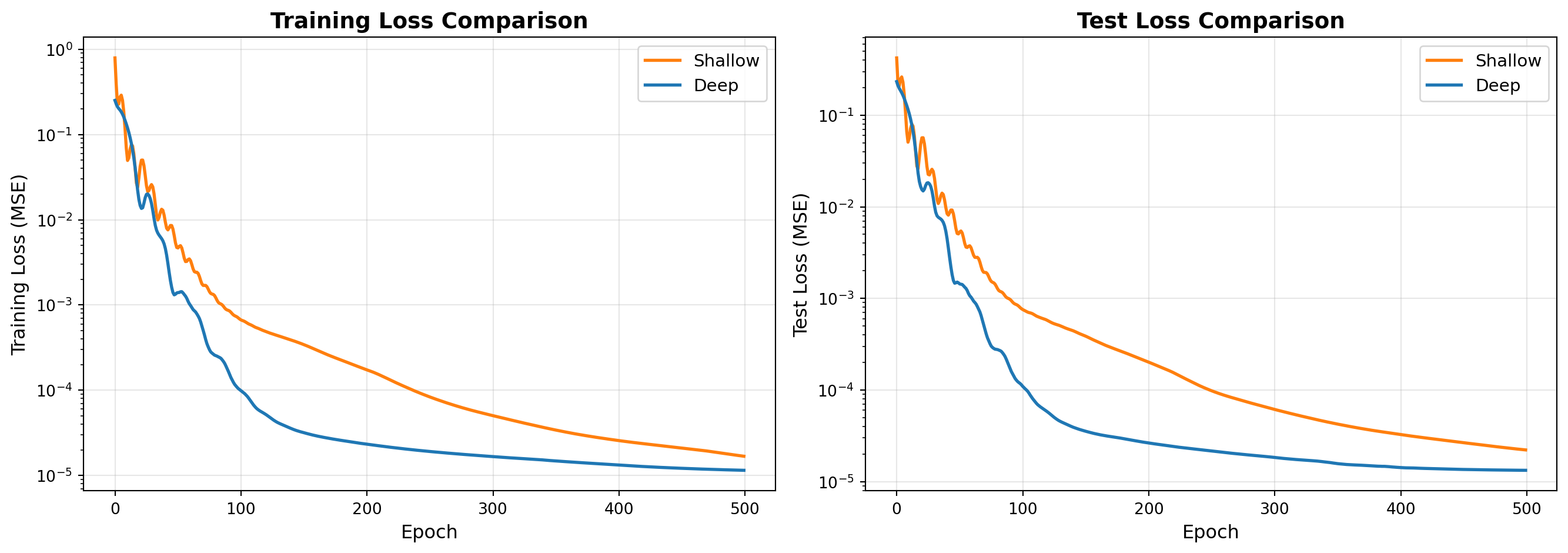
Step 5: Compare Model Performance

Show code 
fig, axes = plt.subplots(1, 2, figsize=(14, 5))
colors = {'Shallow': '#ff7f0e', 'Deep': '#1f77b4'}

# Plot training loss
for name, data in history.items():
    axes[0].plot(data['train_loss'], label=name, linewidth=2, color=colors[name])

axes[0].set_xlabel('Epoch', fontsize=12)
axes[0].set_ylabel('Training Loss (MSE)', fontsize=12)
axes[0].set_title('Training Loss Comparison', fontsize=14, fontweight='bold')
axes[0].legend(fontsize=11)
axes[0].grid(True, alpha=0.3)
axes[0].set_yscale('log')

# Plot test loss
for name, data in history.items():
    axes[1].plot(data['test_loss'], label=name, linewidth=2, color=colors[name])

axes[1].set_xlabel('Epoch', fontsize=12)
axes[1].set_ylabel('Test Loss (MSE)', fontsize=12)
axes[1].set_title('Test Loss Comparison', fontsize=14, fontweight='bold')
axes[1].legend(fontsize=11)
axes[1].grid(True, alpha=0.3)
axes[1].set_yscale('log')

plt.tight_layout()
plt.show()

# Print final metrics
print("\nFinal Performance (after {} epochs):".format(n_epochs))
print("-" * 70)
print(f"{'Model':<15} {'Parameters':<15} {'Train Loss':<15} {'Test Loss':<15}")
print("-" * 70)
for name in models.keys():
    params = count_parameters(models[name])
    train_loss = history[name]['train_loss'][-1]
    test_loss = history[name]['test_loss'][-1]
    print(f"{name:<15} {params:<15,} {train_loss:<15.6f} {test_loss:<15.6f}")


Final Performance (after 500 epochs):
----------------------------------------------------------------------
Model           Parameters      Train Loss      Test Loss      
----------------------------------------------------------------------
Shallow         385             0.000017        0.000022       
Deep            177             0.000012        0.000013

This experiment demonstrates the practical implications of depth versus width in neural network architecture design, showing how deeper networks can achieve competitive performance with fewer parameters.