Gilbert Strang’s Calculus: Big Picture on Derivatives
Video: Big Picture: Derivatives (Gilbert Strang)
Why derivatives matter
Derivatives connect a function to its local behavior: how fast it changes and which way it is heading. This note is a compact map of that idea using the most important functions and the slope viewpoint.
The great functions
These are the core families you keep seeing in calculus:
- Power: \(y=x^n\)
- \(\dfrac{dy}{dx}=n x^{n-1}\)
- Trigonometric:
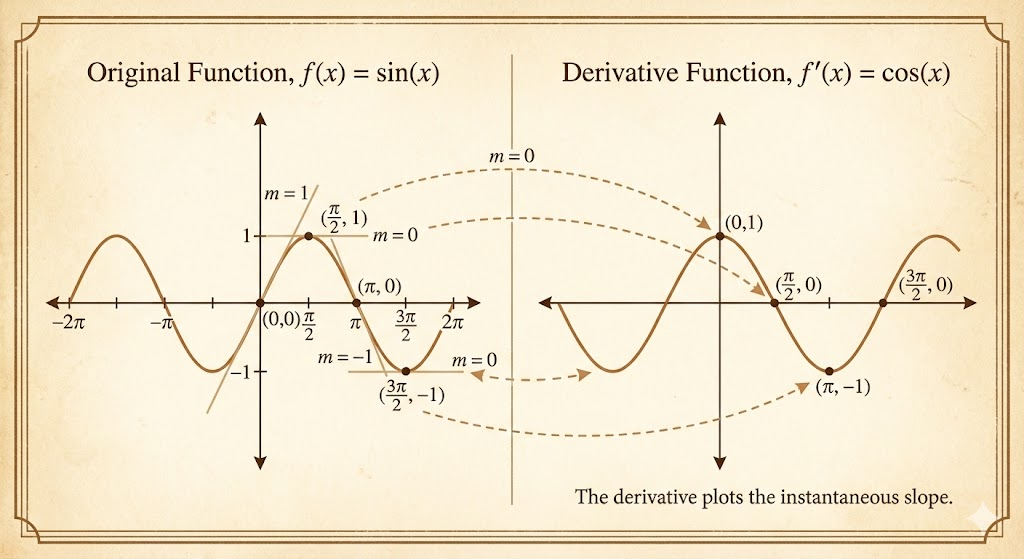
- \(y=\sin x \Rightarrow \dfrac{dy}{dx}=\cos x\)
- \(y=\cos x \Rightarrow \dfrac{dy}{dx}=-\sin x\)
- Exponential:
- \(y=e^x \Rightarrow \dfrac{dy}{dx}=e^x\)
Slope: average vs. instantaneous
Slope is the change in \(y\) over the change in \(x\).
Average slope over a small step \(\Delta x\): \[ \text{Average slope} = \frac{f(x+\Delta x)-f(x)}{\Delta x} \]
Instantaneous slope is the limit as \(\Delta x \to 0\): \[ \frac{dy}{dx}=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x} \]
At the bottom of a curve, the slope is zero.
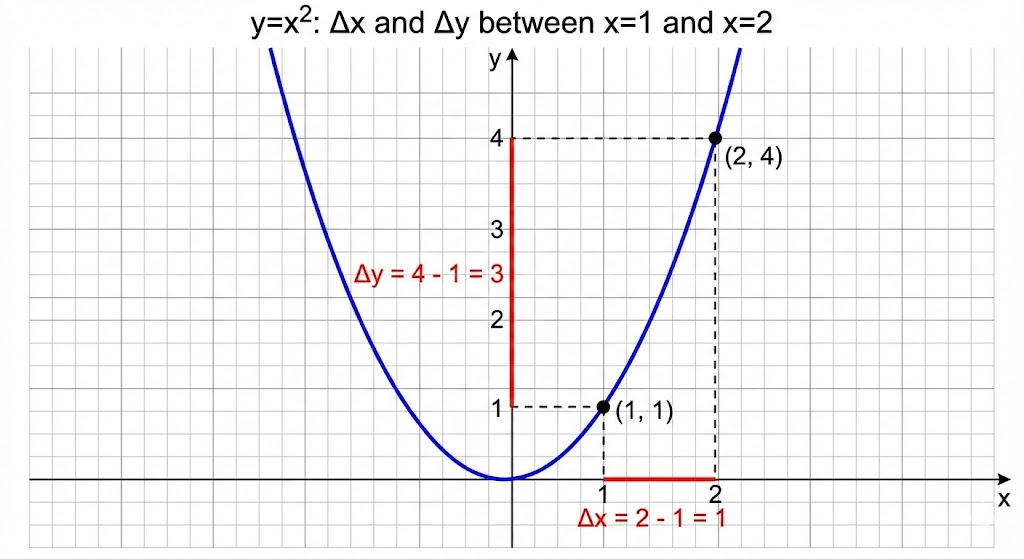
Example: \(f(x)=x^2\)
Compute the instantaneous slope: \[ \lim_{\Delta x \to 0}\frac{(x+\Delta x)^2-x^2}{\Delta x} =\lim_{\Delta x \to 0}\frac{2x\Delta x+\Delta x^2}{\Delta x} =2x \]
So \(f'(x)=2x\).
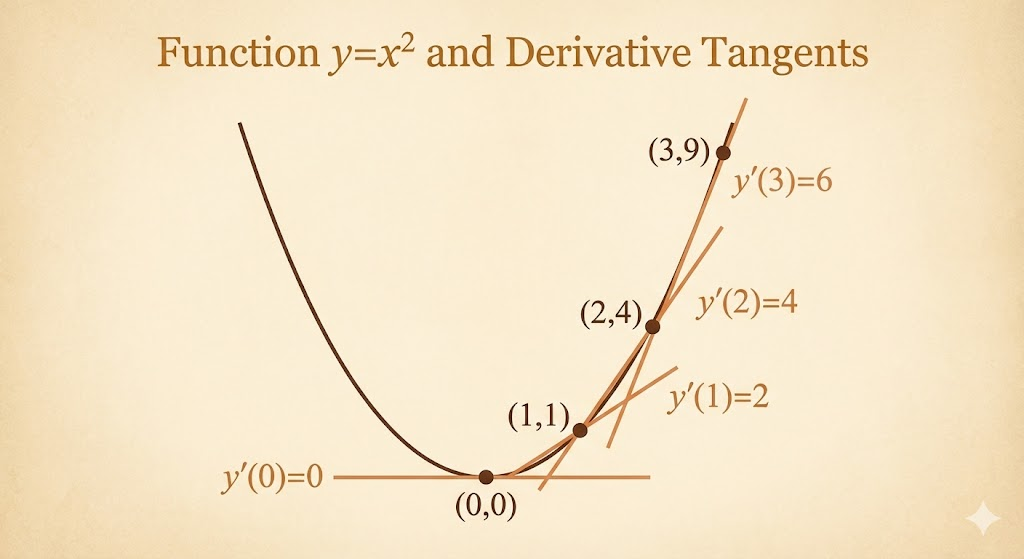
Function and derivative
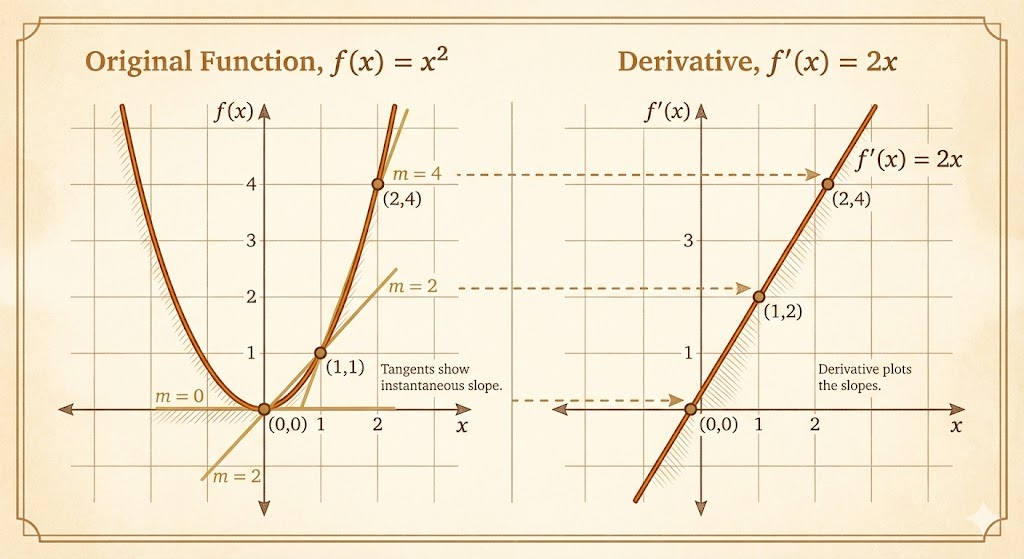
Derivatives are functions too. A curve and its slope curve tell a two-part story.
- \(f(x)=x^2\) and \(f'(x)=2x\)
- \(f(x)=\sin x\) and \(f'(x)=\cos x\)
Takeaway. The derivative is the bridge from shape to change. Once you know the core functions and the slope limit, you can read local behavior directly from a graph.