EE 364A (Convex Optimization): Lecture 4.1 - Operations Preserving Convexity
Operations preserving Convexity
This lecture covers operations that preserve convexity—building complex convex functions from simpler convex pieces.
Review: Basic Operations from Lecture 3
We’ve already seen some fundamental operations in Lecture 3:
- Nonnegative weighted sum: If \(f_1, f_2\) are convex, then \(f_1 + f_2\) is convex
- Nonnegative scaling: If \(f\) is convex and \(\alpha > 0\), then \(\alpha f\) is convex
- Composition with affine mapping: If \(f\) is convex, then \(g(x) = f(Ax + b)\) is convex
Now we’ll extend this toolkit with more powerful operations that preserve convexity.
Pointwise Maximum
if \(f_1,...f_n\) are convex, then \(f(x)=\max(f_1(x),...f_n(x))\) is convex
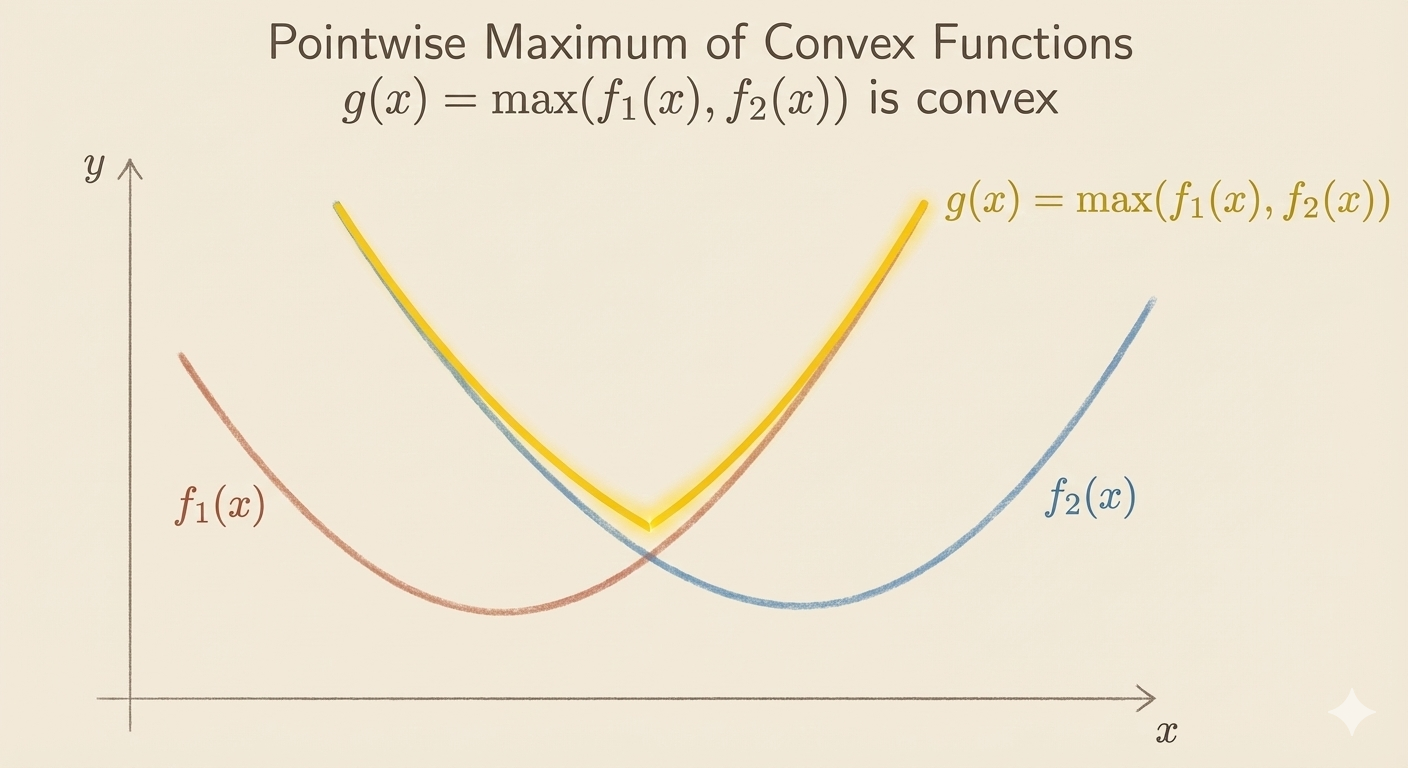
Examples:
- Piecewise-linear function: \(f(x)=\max_{i=1,...m}(a_i^\top x+b_i)\) is convex
- Sum of \(r\) largest components of \(x \in R^n\): \[ f(x)=x_{[1]}+x_{[2]}+...x_{[r]} \] is convex
Pointwise Supremum
if \(f(x,y)\) is convex in \(x\) for each \(y \in A\), then \[ g(x)=\sup_{y \in A}f(x,y) \] is convex.
Examples:
- Support function of a set C: \(S_C(x)=\sup_{y\in C}y^\top x\)
- Distance to farthest point in a set C: \(f(x)=\sup_{y\in C}||y-x||\)
- Maximum eigenvalue of symmetric matrix for \(X \in S^n\), \(\lambda_{\max}(X)=\sup_{||y||_2=1}y^\top Xy\)
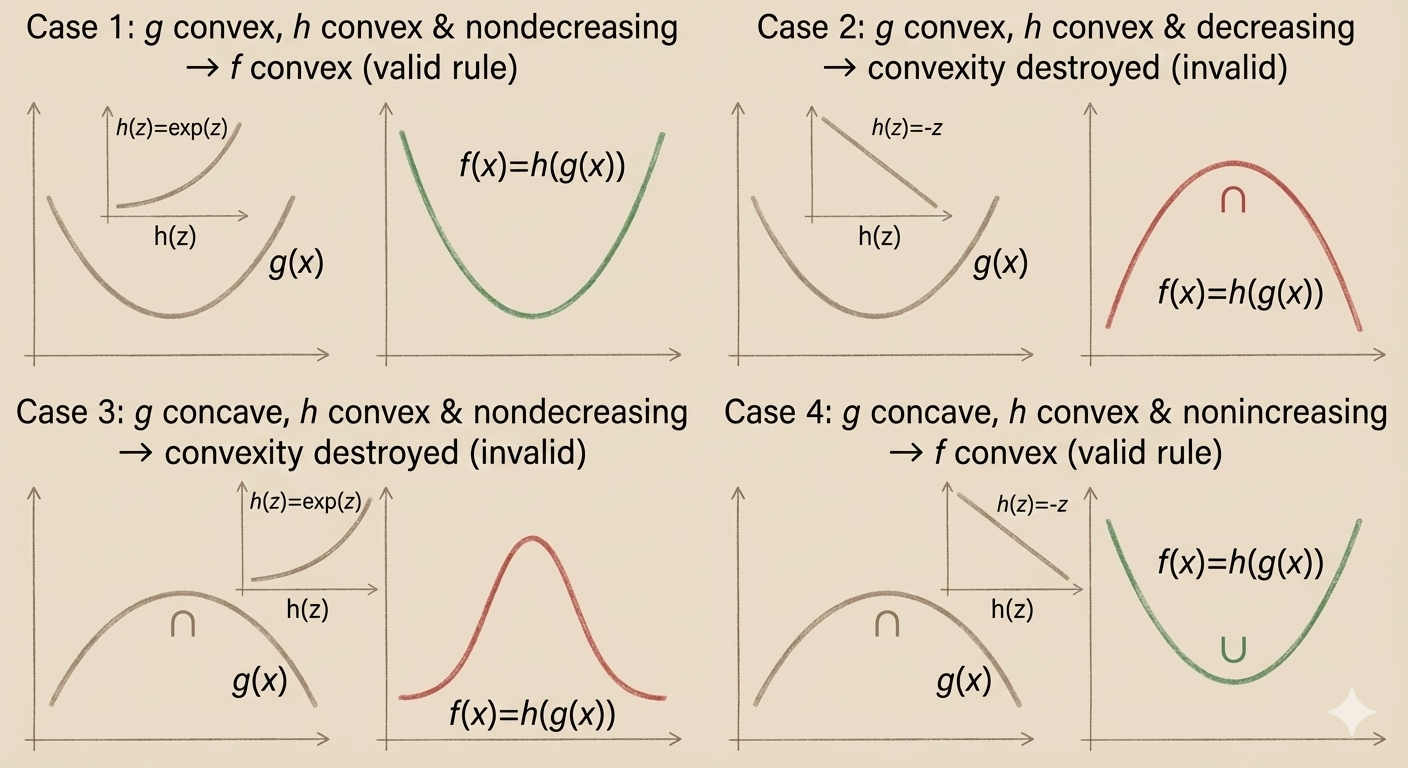
Composition with Scalar Functions
Composition of g: \(R^n \to R\), and h : \(R \to R\)
\(f(x)=h(g(x))\)
is convex if
- g is convex, h is convex, \(\tilde{h}\) nondecreasing
- g is concave, h is convex, \(\tilde{h}\) nonincreasing
Proof
\(f'(x)=h'(g(x))\cdot g'(x)\)
From the general 1st order derivative theorem of \(f_n(x)=f_a(x)\cdot f_b(x)\) is \(f_n'(x)=f_a'(x)\cdot f_b(x)+f_a(x)\cdot f_b'(x)\)
So the second order derivative of \(f(x)\) is:
\(f''(x)=h''(g(x))\cdot g'(x)^2+h'(g(x))g''(x)\)
Examples:
- \(\exp(g(z))\) is convex if \(g(z)\) is convex
- \(\frac{1}{g(z)}\) is convex if \(g(z)\) is concave and positive
Vector Composition (General Rule)
Composition of g: \(R^n \to R^k\) and h: \(R^k \to R\)
\(f(x)=h(g(x))=h(g_1(x),g_2(x),...,g_k(x))\)
is convex if
- case 1: \(g_i\) is convex, h is convex, \(\tilde{h}\) nondecreasing in each argument
- case 2: \(g_i\) is concave, h is convex, \(\tilde{h}\) nonincreasing in each argument
Proof
\[ f''(x)=g'(x)^\top \nabla^2h(g(x))g'(x)+\nabla h(g(x))^\top g''(x) \]
Examples:
- \(\sum_{i=1}^m\log g_i(x)\) is concave if \(g_i(x)\) is concave and positive
- \(\log\sum_{i=1}^m\exp g_i(x)\) is convex if \(g_i(x)\) is convex
Minimization
if \(f(x,y)\) is convex in \((x,y)\) and \(C\) is a convex set, then \[ g(x)=\inf_{y \in C}f(x,y) \] is convex.
Example 1: Quadratic function
\[ f(x,y) = \begin{bmatrix} x \\ y \end{bmatrix}^\top \begin{bmatrix} A & B \\ B^\top & C \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}, \quad Q = \begin{bmatrix}A&B\\B^\top&C\end{bmatrix}\succeq 0,\; C\succ 0 \]
Minimizing over y gives \(g(x)=\inf_yf(x,y)\)
The gradient with respect to y is:
\[ \nabla_y f(x,y) = 2B^\top x + 2C y \]
Setting the gradient to zero: \(2B^\top x + 2C y = 0 \Rightarrow y^*=-C^{-1}B^\top x\)
\[ f(x,y^\star)=x^\top(A-BC^{-1}B^\top)x \]
From Schur complement, \(A-BC^{-1}B^\top \succeq 0\)
From the preservation rule, \(g(x)\) is convex.
Example 2: Distance to a set
Distance to a set: \(\mathrm{dist}(x,S)=\inf_{y\in S}||x-y||\) is convex if S is convex
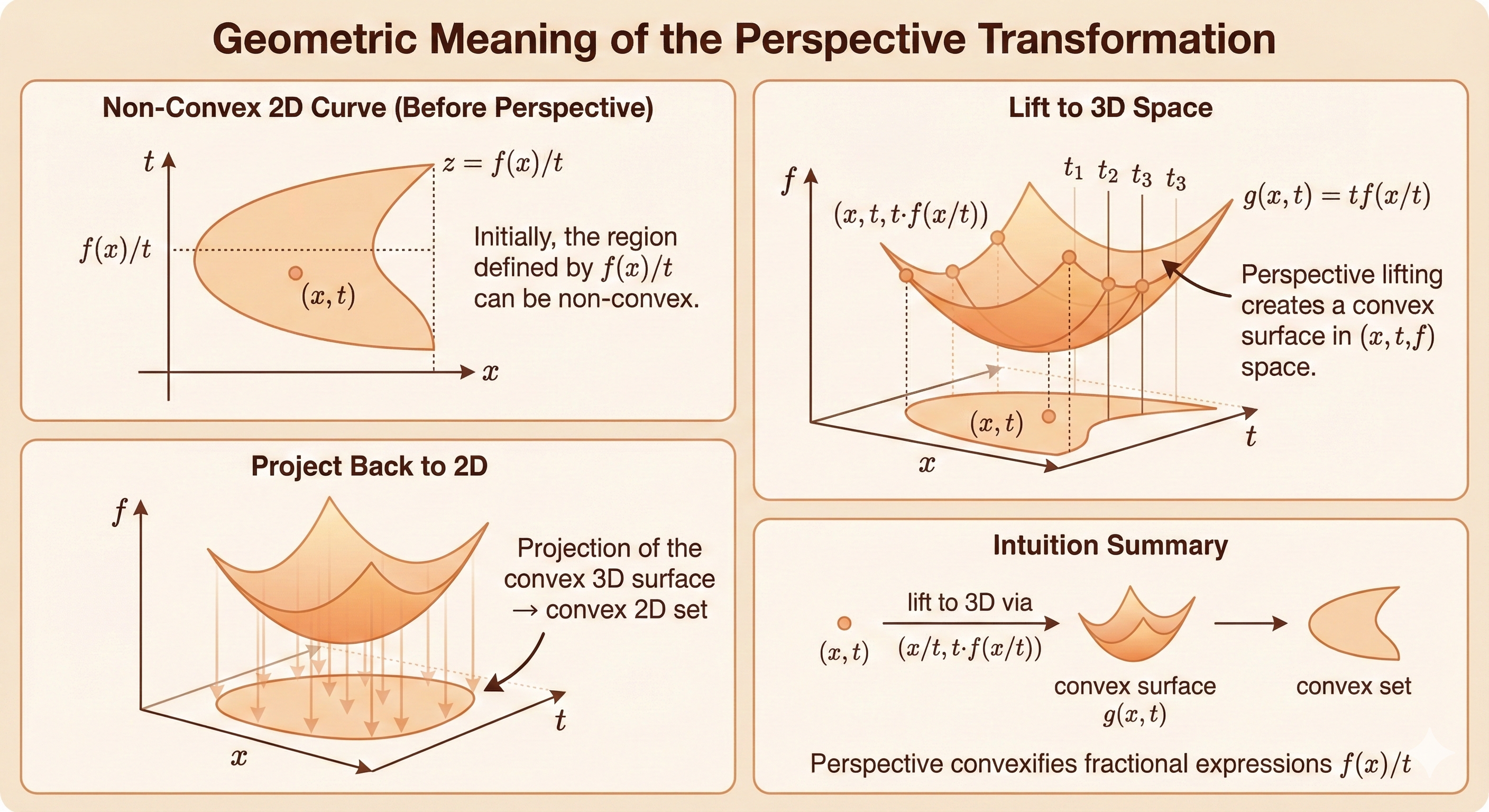
Perspective
The perspective function of a function \(f: R^n \to R\) is the function \(g: R^n \times R \to R\)
\[ g(x,t)=tf(x/t), \quad \mathrm{dom}\, g=\{(x,t) |x/t\in \mathrm{dom}\,f,t> 0 \} \]
\(g\) is convex if \(f\) is convex.

Examples:
- \(f(x)=x^\top x\) is convex; hence \(g(x,t)=x^\top x/t\) is convex for \(t> 0\)
- \(f(x)=-\log x\) is convex, so \(g(x,t)=t\log t- t \log x\) is convex on \(R_{++}^2\)
- if f is convex, then \(g(x)=(c^\top x+b)f((Ax+b)/(c^\top x+d))\) is convex on \[ \{x \mid c^\top x + b > 0,\ (Ax+b)/(c^\top x + d) \in \mathrm{dom}\, f \} \]