EE 364A (Convex Optimization): Lecture 5.2 - Monotonicity and Convexity with Generalized Inequalities
Convex Optimization Textbook - Chapter 3.6 (page 122)
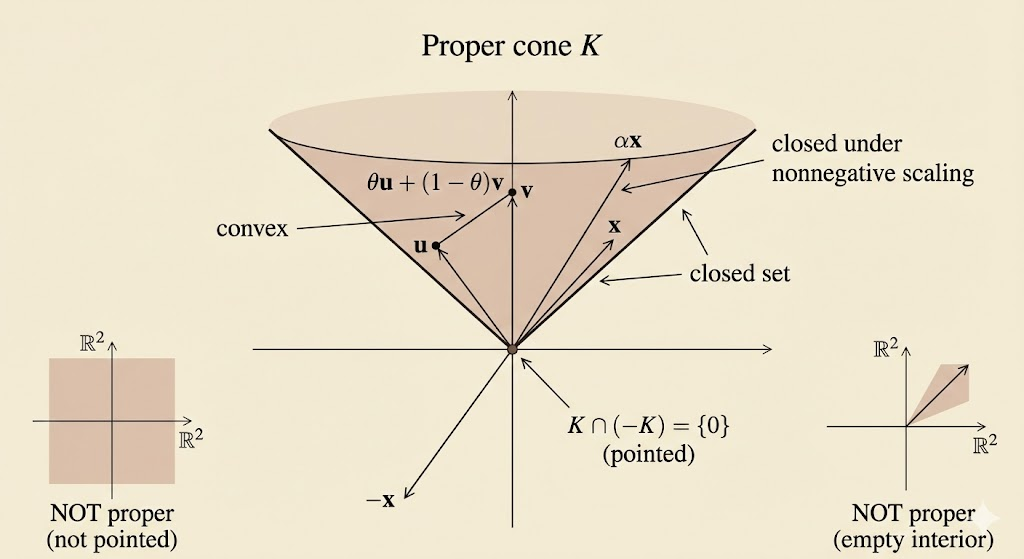
Proper Cone
A proper cone has five properties:
- Cone: \(x \in K,\ \alpha \ge 0 \Rightarrow \alpha x \in K\)
- Convex: \(x,y \in K,\ 0 \le \theta \le 1 \Rightarrow \theta x + (1-\theta)y \in K\)
- Closed
- Pointed
- Non-empty interior
A cone \(K\subseteq\mathbb{R}^n\) is proper if it is convex, closed, pointed, and has nonempty interior.
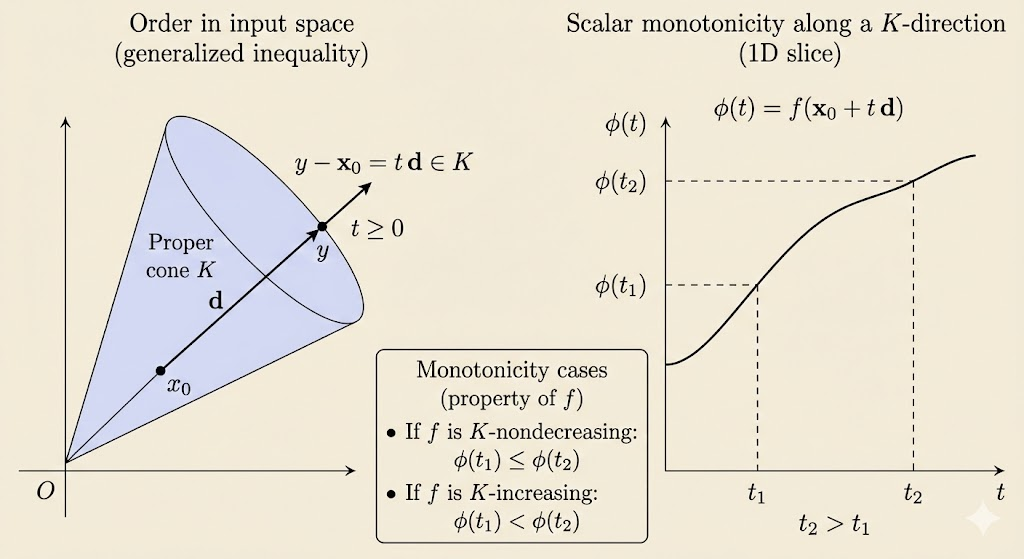
Monotonicity with respect to generalized inequality
Suppose \(K \subseteq \mathbb{R}^n\) is a proper cone with associated generalized inequality \(\preceq_K\). A function \(f:\mathbb{R}^n \to \mathbb{R}\) is called K-nondecreasing if:
\[ x \preceq_K y \Longrightarrow f(x)\le f(y) \]
and K-increasing if:
\[ x \preceq_K y, x\ne y \Longrightarrow f(x)< f(y) \]
Examples
Monotone Vector Functions
A function \(f:\mathbb{R}^n \to \mathbb{R}\) is nondecreasing with respect to \(\mathbb{R}_+^n\) iff:
\[ x_1\le y_1,...,x_n \le y_n \Longrightarrow f(x)\le f(y) \]
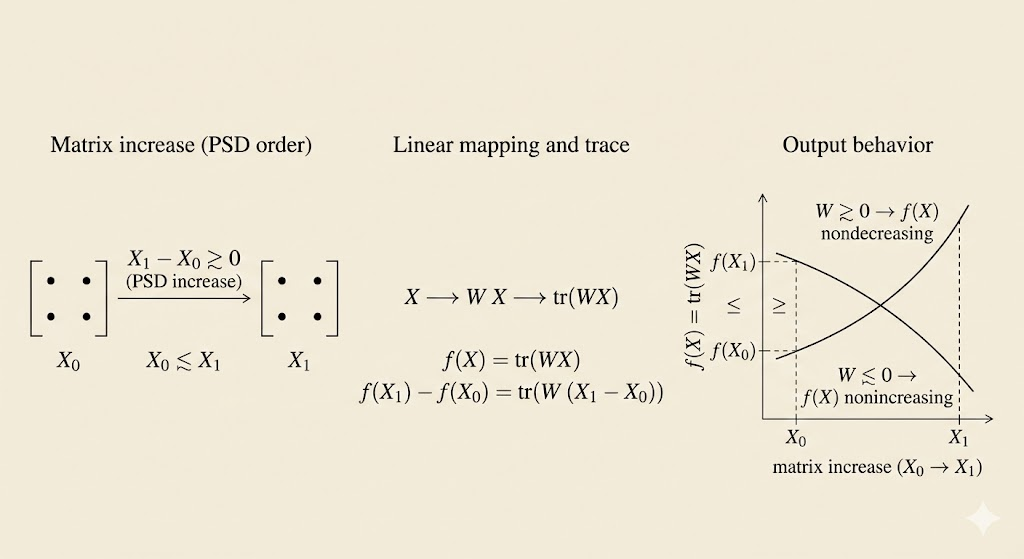
Matrix Monotone Functions
A function \(f:S^n \to \mathbb{R}\) is called matrix monotone (increasing, decreasing) if it is monotone with respect to the positive semidefinite cone.
Examples:
- \(\mathrm{tr}(WX) \quad |W \in S^n\):
- \(W \succeq 0\): matrix nondecreasing
- \(W \succ 0\): matrix increasing
- \(W \preceq 0\): matrix nonincreasing
- \(W \prec 0\): matrix decreasing
- \(\mathrm{tr}(X^{-1})\) is matrix decreasing on \(S_{++}^n\)
- \(\mathrm{det}X\) is matrix increasing on \(S_{++}^n\), and matrix nondecreasing on \(S_{+}^n\)
Gradient Condition for Monotonicity
For differentiable function \(f: \mathbb{R} \to \mathbb{R}\), with convex domain, is nondecreasing iff \(f'(x)\ge 0 \quad \forall \, x\in \mathrm{dom }f\), and increasing if \(f'(x)> 0 \quad \forall \, x\in \mathrm{dom }f\) (For the strict condition, the converse is not true.).
For example, \(f(x)=x^3\) is increasing, but the derivative is \(3x^2\). When \(x=0\), the derivative is 0.
These conditions can be readily extended to the case of monotonicity with respect to a generalized inequality. A differentiable function \(f\), with convex domain, is K-nondecreasing iff:
\[ \nabla f(x) \succeq_{K^*} 0 \quad \forall \,x \in \mathrm{dom }f \]
The gradient should be non-negative in the dual inequality.
For the strict case, if \(\nabla f(x) \succ_{K^*} 0 \quad \forall \,x \in \mathrm{dom }f\), then \(f\) is K-increasing.
Proof
Sufficient Condition:
Assume \(f\) satisfies \(\nabla f(x) \succeq_{K^*} 0 \quad \forall \,x \in \mathrm{dom }f\), and there exists \(x,y\) such that \(x \preceq_{K} y\) and \(f(y)< f(x)\). By differentiability there exists a \(t \in [0,1]\) with:
\[ \frac{d}{dt}f(x+t(y-x))=\nabla f(x+t(y-x))^\top(y-x) <0 \]
Since \(y-x \in K\), so \(\nabla f(x+t(y-x)) \notin K^*\), which contradicts our assumption that \(\nabla f(x) \succeq_{K^*} 0\) everywhere.
Necessary Condition:
Assume \(\nabla f(x) \succeq_{K^*} 0\) doesn’t hold for \(x=z\). Then there exists a \(v \in K\) with \(\nabla f(z)^\top v < 0\), which means \(f\) is not K-nondecreasing.
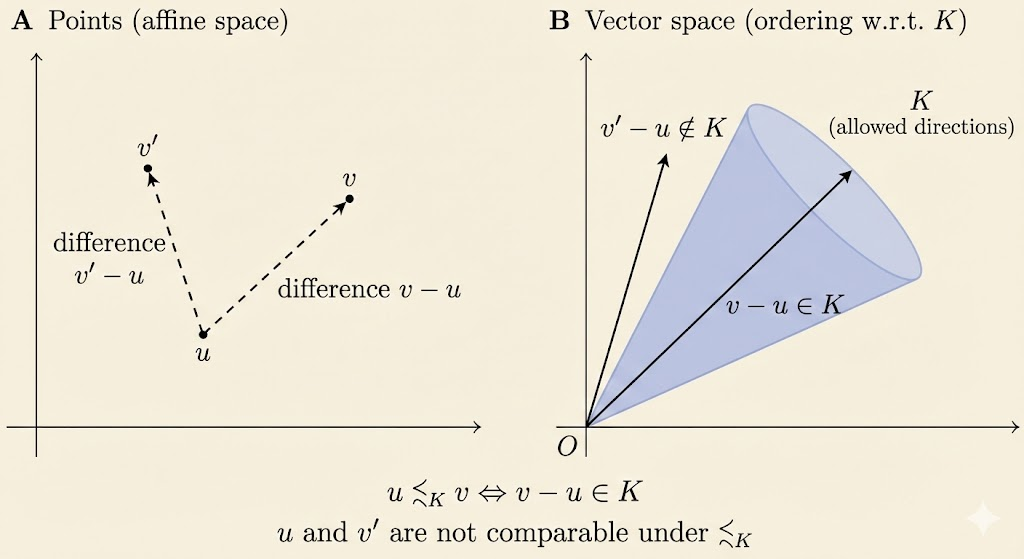
Convexity with respect to a general inequality
Suppose \(K \subseteq \mathbb{R}^m\) is a proper cone with associated generalized inequality \(\preceq _K\). We say \(f:\mathbb{R}^n\to \mathbb{R}^m\) is K-convex if for all \(x,y\) and \(0 \le \theta \le 1\):
\[ f(\theta x+(1-\theta) y)\preceq_K \theta f(x)+(1-\theta)f(y) \]
The function is strictly K-convex if:
\[ f(\theta x+(1-\theta) y)\prec_K \theta f(x)+(1-\theta)f(y) \]
for all \(x \ne y\) and \(0 \le \theta < 1\).
Examples
Matrix Convexity
Matrix Inequality:
For \(A \in S^n, B \in S^n\):
- \(A \succ B\) if \(A-B\) is positive definite
- \(A \succeq B\) if \(A-B\) is positive semidefinite
- \(A\prec B\) if \(A-B\) is negative definite
- \(A \preceq B\) if \(A-B\) is negative semidefinite
- Otherwise, not comparable
Suppose \(f\) is a symmetric-valued function, e.g., \(f:\mathbb{R}^n \to S^m\). The function \(f\) is convex with respect to matrix inequality if:
\[ f(\theta x+(1-\theta)y) \preceq \theta f(x)+(1-\theta)f(y) \]
for all \(x\) and \(y\), and \(0 \le \theta \le 1\).
\(f\) is strictly matrix convex if \(f(\theta x+(1-\theta)y) \prec \theta f(x)+(1-\theta)f(y)\) for all \(x \ne y\) and \(0 \le \theta \le 1\).
Examples:
- \(f(X)=XX^\top\) where \(X \in \mathbb{R}^{n \times m}\)
- \(f(X)=X^p\) where \(X \in S_{++}^n\), \(1\le p\le2\) or \(-1 \le p\le 0\)
- \(f\) is matrix concave for \(0 \le p \le1\)
- \(f(X)=e^X\) is NOT matrix convex on \(S^n\) for \(n \ge 2\)
Dual characterization of K-convexity
A function \(f:\mathbb{R}^n \to \mathbb{R}^m\) is K-convex iff \(\forall w \succeq _{K^*} 0\), \(w^\top f\) is convex (in the ordinary sense).
\(f\) is strictly K-convex if \(w^\top f\) is strictly convex for every nonzero \(w\) in \(K^*\).
Differentiable K-convex functions
A differentiable function \(f\) is K-convex iff:
- Its domain is convex
- For all \(x,y \in \mathrm{dom } f\):
\[ f(y)\succeq_K f(x)+Df(x)(y-x) \]
where \(Df(x)\) is the Jacobian matrix of \(f\) at \(x\).
Composition Theorem
Many of the results on composition can be generalized to K-convexity. For example, if:
- \(g:\mathbb{R}^n \to \mathbb{R}^p\) is K-convex
- \(h: \mathbb{R}^p \to \mathbb{R}\) is convex
- \(\tilde{h}\) is K-nondecreasing (extended-value extension of \(h\))
The condition that \(\tilde h\) is K-nondecreasing implies \(\mathrm{dom}\,h - K = \mathrm{dom}\,h\).
Then \(h\circ g\) is convex.