MIT 18.065: Lecture 17 - Rapidly Decreasing Singular Values
Rapidly decreasing singular values
When singular values decay quickly, a matrix behaves as if it were low rank. This lecture links rank facts, numerical rank, image compression, structured matrices, and Sylvester equations through the lens of singular-value decay.
Facts about singular values and rank
For an \(n\times n\) matrix \(X\), \[ \sigma_1(X) \ge \sigma_2(X) \ge \dots \ge \sigma_n(X) \ge 0. \] - If \(\sigma_k(X)>0\) and \(\sigma_{k+1}(X)=0\), then \(\mathrm{rank}(X)=k\). - Rank-\(k\) matrices admit the outer‑product form \[ X = u_1 v_1^\top + \dots + u_k v_k^\top. \] - The column space and row space both have dimension \(k\).
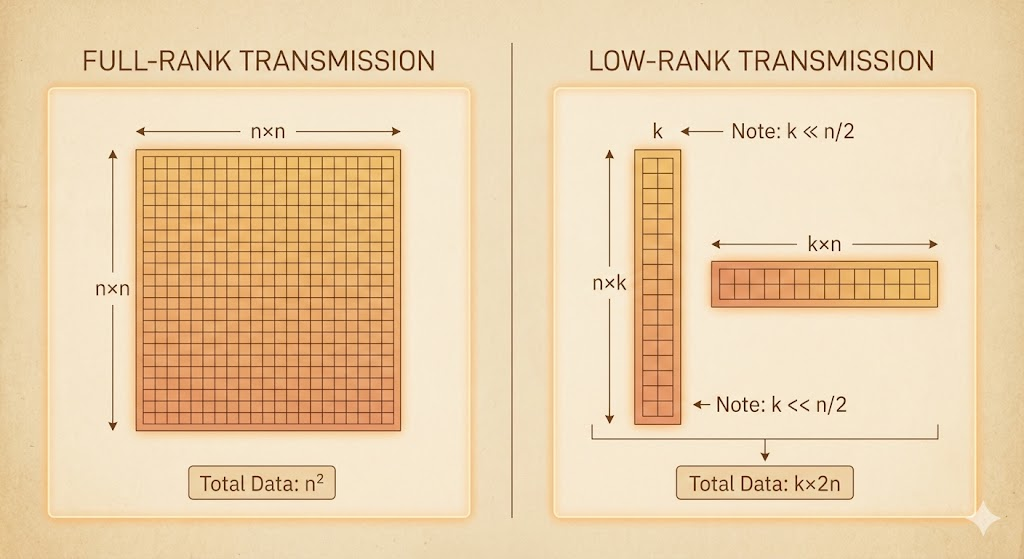
Image compression by low rank
Suppose we have an image of size \(n\times n\).
- Full‑rank storage: \(n^2\) numbers.
- Rank‑\(k\) factorization: store \(U\in\mathbb{R}^{n\times k}\) and \(V\in\mathbb{R}^{n\times k}\), i.e. \(k\times 2n\) numbers.
In practice we require \(k \ll n/2\) to get real compression gains.
Numerical rank
Exact rank is brittle under noise. We define numerical rank with a tolerance \(0<\varepsilon<1\): \[ \mathrm{rank}_\varepsilon(X)=k \quad\text{if}\quad \sigma_{k+1}(X) \le \varepsilon\,\sigma_1(X) \quad\text{and}\quad \sigma_k(X) > \varepsilon\,\sigma_1(X). \] Numerical rank measures how many singular values are meaningfully large, ignoring tiny values caused by noise or round‑off error.
Numerically low‑rank matrices
Hilbert matrix
\[ H_{j,k}=\frac{1}{j+k-1} \] A \(5\times5\) Hilbert matrix: \[ \begin{bmatrix} 1 & 0.5 & 0.33333333 & 0.25 & 0.2 \\ 0.5 & 0.33333333 & 0.25 & 0.2 & 0.16666667 \\ 0.33333333 & 0.25 & 0.2 & 0.16666667 & 0.14285714 \\ 0.25 & 0.2 & 0.16666667 & 0.14285714 & 0.125 \\ 0.2 & 0.16666667 & 0.14285714 & 0.125 & 0.11111111 \end{bmatrix} \] Hilbert matrices are notoriously ill‑conditioned and have rapidly decaying singular values.
Vandermonde matrix
\[ \begin{bmatrix} 1 & x_1 & \dots & x_1^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & \dots & x_n^{n-1} \end{bmatrix} \] Vandermonde matrices can also be ill‑conditioned, with strong singular‑value decay depending on the node distribution.
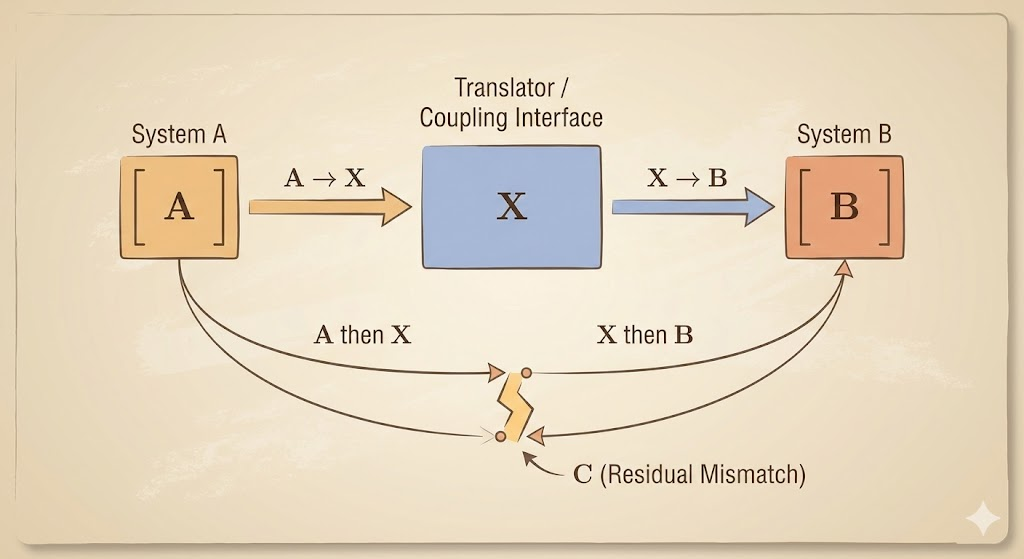
The world is Sylvester
Many real problems involve operators acting from the left and right. This is captured by the Sylvester equation \[ AX - XB = C. \] Its solutions often exhibit low‑rank structure when the spectra of \(A\) and \(B\) are well separated, which explains why singular values can decay rapidly.
From a coordination viewpoint, \(X\) connects two systems governed by \(A\) and \(B\), and \(C\) measures their mismatch. When \(A\) and \(B\) are compatible, \(C\) is small; when not, the system is numerically sensitive.
Theorem (singular value decay bound)
If \(X\) satisfies \(AX - XB = C\), then \[ \sigma_{rk+1}(X) \le Z_k(E,F)\,\sigma_1(X), \] where - \(E\) and \(F\) are the eigenvalue sets of \(A\) and \(B\), - \(r=\mathrm{rank}(C)\), - \(Z_k(E,F)\) is the Zolotarev number, which measures how well the two spectral sets can be separated by low‑degree rational functions.
This theorem explains why spectral separation drives fast singular‑value decay in Sylvester‑type problems.
Takeaway. Rapidly decreasing singular values justify low‑rank approximations, enable compression, and explain why many structured matrix equations are numerically low rank even when they are full rank algebraically.