Goodfellow Deep Learning — Chapter 10.7: The Challenge of Long-Term Dependencies
The fundamental challenge of long-term dependencies is not representational capacity but the difficulty of training recurrent networks.
During backpropagation through time, gradients must be propagated across many steps, causing:
- vanishing gradients (the common case), where the gradient shrinks exponentially and the network cannot learn dependencies across distant time steps
- exploding gradients (rare but severe), where the gradient grows exponentially and destabilizes learning
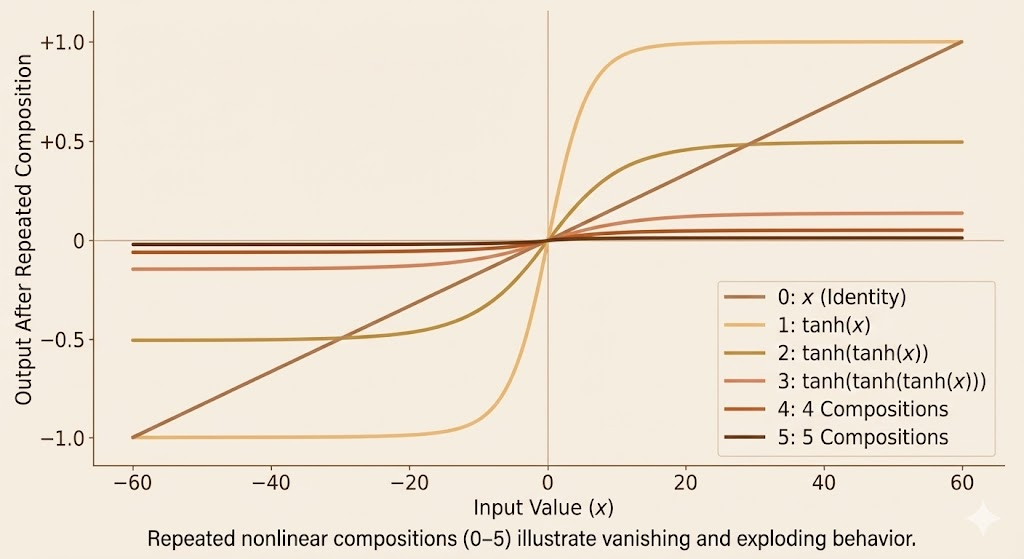
The figure shows how repeatedly applying the same nonlinear function causes saturation or steep amplification. Although the x-axis is not time, these compositions mirror the effect of many RNN time steps, explaining why gradients vanish or explode during long-term dependency learning.
Mathematical Analysis
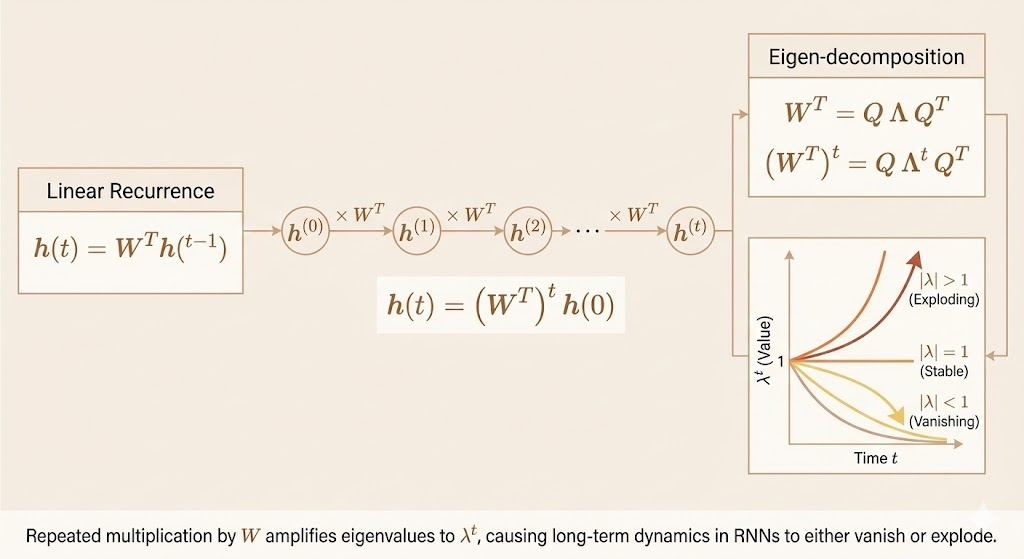
\[ h^{t} = W h^{t-1} \tag{10.36} \]
Hidden state after \(t\) steps can be written as the repeated application of the same linear transformation:
\[ h^{t} = W^{t} h^{0} \tag{10.37} \]
showing that long-term behavior is governed by powers of the transition matrix.
\[ W = Q\Lambda Q^{\top} \tag{10.38} \]
We can analyze its dynamics in the eigenbasis if \(W\) is diagonalizable:
\[ h^{t} = Q \Lambda^{t} Q^{\top} h^{0} \tag{10.39} \]
Each eigenvalue raised to the \(t\)-th power either shrinks (vanishing) or grows (exploding), explaining instability over long time horizons.