Goodfellow Deep Learning — Chapter 18: Confronting the Partition Function
Unnormalized energy-based models are powerful because they define flexible distributions, but they hide a hard computational problem: the partition function. This chapter focuses on how the partition function appears in gradients and what techniques allow learning without computing it exactly.
Partition function
An unnormalized model must be normalized by dividing by a partition function \(Z(\theta)\): \[ p(x;\theta)=\frac{1}{Z(\theta)}\tilde{p}(x;\theta) \] - Continuous variables: \(\int \tilde{p}(x)\,dx\) - Discrete variables: \(\sum_x \tilde{p}(x)\)
Log-likelihood Gradient
The log-likelihood gradient splits into two terms: one encourages high probability on data, the other adjusts the global normalization. This split is the core difficulty in training energy-based models.
The gradient of the log-likelihood has a term corresponding to the gradient of the partition function: \[ \nabla_\theta \log p(x;\theta)=\nabla_\theta \log \tilde{p}(x;\theta)-\nabla_\theta \log Z(\theta) \] \(\log(a/b)=\log(a)-\log(b)\quad a>0,b>0\)
Looking at the gradient of \(\log Z\): \[ \nabla_\theta \log Z \\ =\frac{\nabla_\theta Z}{Z}\\ =\frac{\nabla_\theta\sum_x \tilde{p}(x)}{Z}\\=\frac{\sum_x \nabla_\theta \tilde{p}(x) }{Z} \]
Because \(\nabla_\theta \log Z=\nabla_\theta Z \cdot \frac{\partial \log Z}{\partial Z}\) and \(\frac{\partial \log Z}{\partial Z}=\frac{1}{Z}\).
If the model guarantees \(p(x)>0\), we can substitute \(\exp \log(\tilde{p}(x))\) for \(\tilde{p}(x)\): \[ \frac{\sum_x \nabla_\theta \exp \log\tilde{p}(x) }{Z}=\\ \frac{\sum_x {p}(x) \nabla_\theta \log \tilde{p}(x) }{Z}=\\ E_{x\sim p(x)} \nabla_\theta \log \tilde{p}(x) \] This also holds for continuous distributions.
Stochastic Maximum likelihood and contrastive divergence
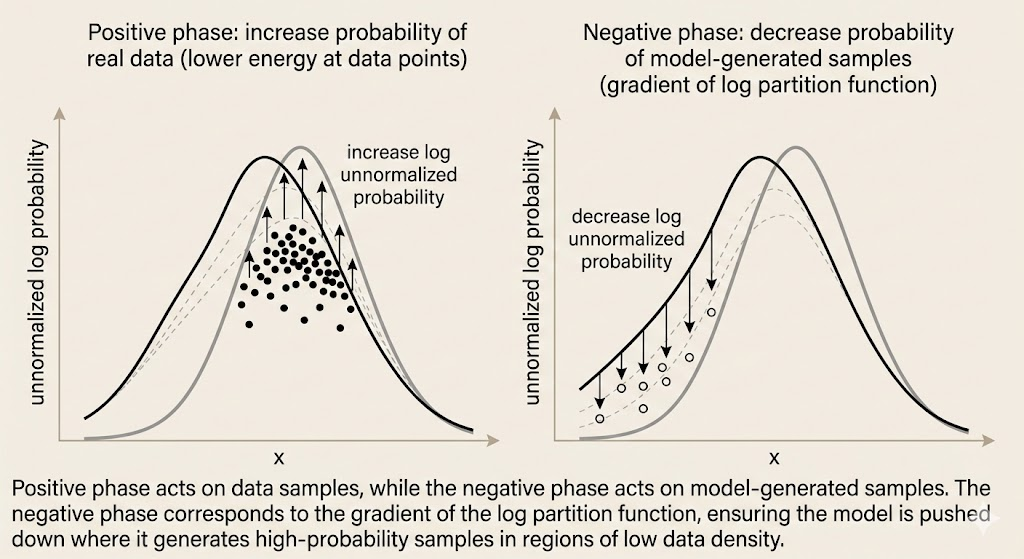
Objective
We train an energy-based model \(p_\theta(x) = \frac{e^{-E(x;\theta)}}{Z(\theta)}\) by maximum likelihood estimation (MLE), i.e., maximizing the log-likelihood of the training data: \(\max_\theta \; \mathbb{E}_{x \sim p_{\text{data}}}\big[\log p_\theta(x)\big]\). The goal is density modeling, not classification: real data should have high probability, while non-data (noise) should have low probability.
Gradient decomposition
The log-likelihood gradient decomposes naturally into two terms: \[ \nabla_\theta \log p_\theta(x) = -\nabla_\theta E(x;\theta) + \nabla_\theta \log Z(\theta), \] \[ \nabla_\theta \log Z(\theta) = \mathbb{E}_{x' \sim p_\theta}\big[\nabla_\theta E(x';\theta)\big]. \] - Positive phase (data-driven): the first term - Negative phase (model-driven): the second term, arising from the partition function
Training method
Positive phase (data-driven): - Sample \(x \sim p_{\text{data}}\). - Increase the (unnormalized) log probability at data points. - Equivalently, lower the energy of real data.
Negative phase (model-driven): - Sample \(x' \sim p_\theta\) using MCMC (e.g., Gibbs sampling). - Decrease the (unnormalized) log probability at model-sampled points. - Equivalently, raise the energy of model-generated samples.
Parameter update: \[ \theta \leftarrow \theta + \eta \left( \mathbb{E}_{p_{\text{data}}}[-\nabla_\theta E(x)] - \mathbb{E}_{p_\theta}[-\nabla_\theta E(x)] \right). \]
Pseudo Likelihood
Pseudolikelihood is an approximation to maximum likelihood for undirected models that avoids computing the partition function. Instead of maximizing the joint log-likelihood \(\log p(x)\), it maximizes the sum of conditional log-probabilities: \(\sum_{i=1}^n \log p(x_i \mid x_{-i})\). Each conditional probability only requires local normalization over \(x_i\), so the global partition function \(Z\) cancels out. This reduces computational complexity from exponential to linear in the number of variables.
Pseudolikelihood is asymptotically consistent, but with finite data it may fail to capture global dependencies, making it less accurate than true maximum likelihood in strongly coupled systems.
Score Matching and Ratio Matching
These are alternative training methods that avoid computing the partition function.
Score Matching trains a model by matching the gradient of the log-density with respect to the input, \(\nabla_x \log p(x)\), rather than the density itself. Because the partition function disappears when differentiating with respect to \(x\), score matching avoids MCMC and negative-phase sampling. It is well-suited for continuous data, but not applicable to discrete variables.
Ratio Matching extends the same idea to discrete and binary data. Instead of matching gradients, it matches local probability ratios between a data point and a slightly perturbed version of it. The partition function cancels in these ratios, enabling efficient training without global normalization. These methods replace global likelihood matching with local consistency constraints, trading generality for computational efficiency.
Noise-Contrastive Estimation
Noise-Contrastive Estimation reformulates density estimation for unnormalized models as a binary classification problem between data samples and noise samples. A noise distribution is introduced, and the model is trained to distinguish data from noise using logistic regression on the log-density ratio. By learning this classifier, the model parameters (and the partition function) can be estimated without explicitly computing the partition function.
NCE is asymptotically consistent under suitable conditions, but its effectiveness depends critically on the choice of the noise distribution. It works well when the classification task remains nontrivial, and is less effective in high-dimensional or highly structured data where simple noise makes the task too easy.
Estimating and Comparing Partition Functions
This section addresses how to compare models and estimate partition functions in energy-based (undirected) models, where the normalization constant \(Z(\theta)\) is generally intractable. While many training methods (e.g., NCE, score matching, ratio matching) avoid computing \(Z\), model evaluation and comparison require it, since normalized likelihoods depend on the partition function. Comparing two models only requires the ratio of their partition functions, not their absolute values.
A natural approach is importance sampling, which estimates \(Z\) using samples from a proposal distribution. However, in high-dimensional or multimodal settings, importance sampling suffers from severe weight degeneracy when the proposal and target distributions have little overlap, leading to extremely high variance.
To address this, Annealed Importance Sampling (AIS) introduces a sequence of intermediate distributions that smoothly interpolate between an easy-to-sample distribution and the target model. By estimating a product of small, stable importance ratios, AIS provides a practical and reliable way to estimate partition function ratios in high dimensions. As a result, AIS has become the standard tool for evaluating energy-based models such as RBMs.