Goodfellow Deep Learning — Chapter 10.8: Echo State Networks
Deep Learning Book - Chapter 10.8 (page 396)
Spectral radius is the maximum eigenvalue: \(\max(\lambda_i)\).
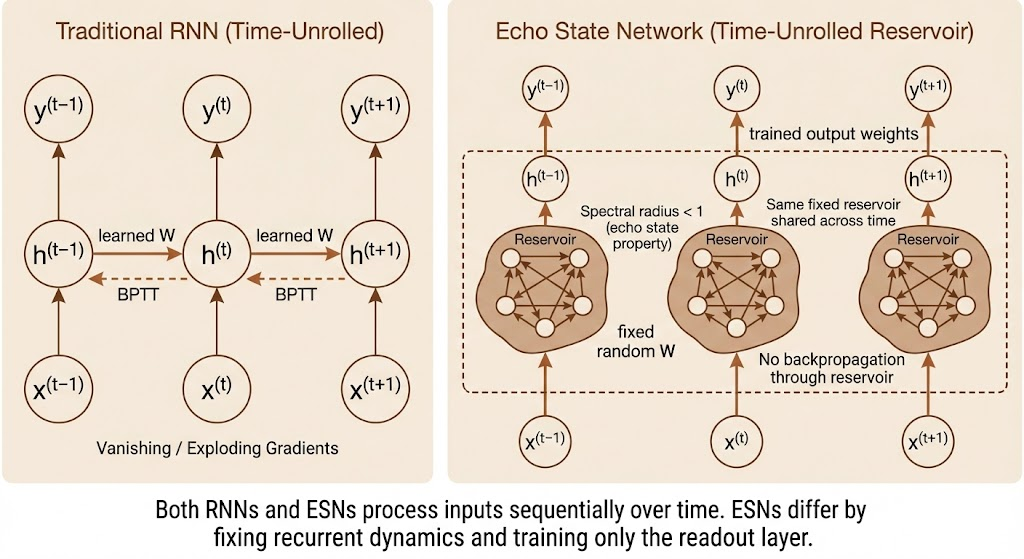
Echo State Networks (ESNs) address the difficulty of learning long-term dependencies in recurrent neural networks by fixing the recurrent weights and training only the output weights. The recurrent network is viewed as a dynamical system, designed so that its hidden state forms a rich, stable representation of the input history.
A key concept is the spectral radius of the recurrent Jacobian (or weight matrix), defined as the maximum absolute eigenvalue. When the spectral radius is less than one, small perturbations in the hidden state contract over time; when it is greater than one, perturbations grow exponentially. Setting the spectral radius close to one places the system near the boundary between stability and instability, enabling the network to retain information over longer time spans.
In ESNs, the recurrent dynamics act as a reservoir that nonlinearly transforms the entire input history into a fixed-dimensional hidden state. Learning is then reduced to a simple supervised problem, typically linear regression from hidden states to outputs, which avoids backpropagation through time.
Overall, ESNs demonstrate that long-term temporal structure can be captured by carefully designed recurrent dynamics rather than learned recurrent weights, though learning long-term dependencies remains a central challenge in deep learning.