Gilbert Strang’s Calculus: Max, Min, and Second Derivative
Video: Max and Min and Second Derivative (Gilbert Strang)
Big idea
The first derivative locates where slope is zero (candidates for max or min). The second derivative tells the curve’s bending direction, so we can decide whether that point is a maximum or minimum.
Speed, slope, and acceleration
- Position/height: \(f(t)\) describes where you are.
- Speed/slope: \(f'(t)\) is the instantaneous rate of change.
- Acceleration/bending: \(f''(t)\) tells how the slope itself changes.
Example: if \(f(x)=x^2\), then \[ f'(x)=2x,\qquad f''(x)=2. \] The constant positive second derivative says the curve bends upward everywhere.

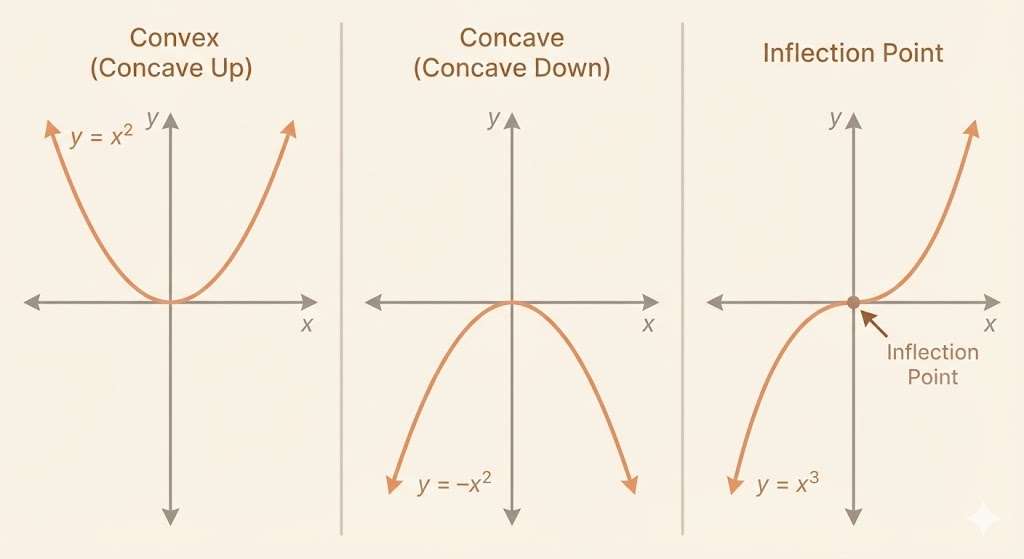
Convex, concave, and inflection
- If \(f''(x) > 0\), the slope is increasing and the graph bends upward (convex).
- If \(f''(x) < 0\), the slope is decreasing and the graph bends downward (concave).
- An inflection point is where the bending changes direction, typically where \(f''(x)=0\).
Example 1: \(y=\sin x\)
- \(y' = \cos x\)
- \(y'' = -\sin x\)
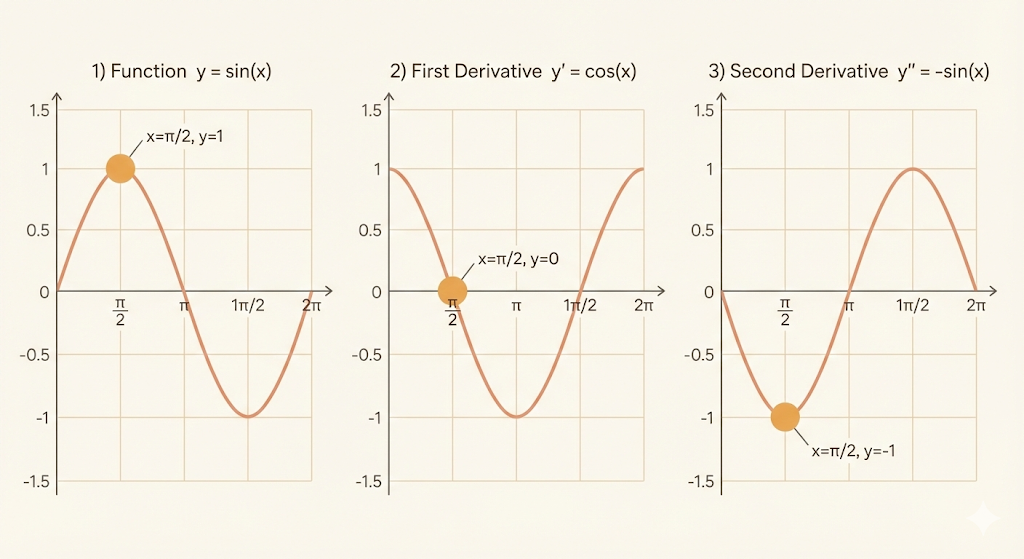
Maximum
At \(x=\pi/2\), \(y=1\) and \(y'=0\). Since \(y''=-1<0\), the curve bends downward, so this is a local maximum.
Inflection point
At \(x=\pi\), \(y''=0\) and the bending changes sign. This is an inflection point.
Minimum
At \(x=3\pi/2\), \(y=-1\) and \(y'=0\). Since \(y''=1>0\), the curve bends upward, so this is a local minimum.
Example 2: \(y=x^3-x^2\)
- \(y' = 3x^2-2x = x(3x-2)\)
- \(y'' = 6x-2\)
Set \(y'=0\): \[ 3x^2-2x=0 \quad\Rightarrow\quad x=0,\; x=\tfrac{2}{3}. \]
- At \(x=0\), \(y''=-2<0\), so this is a local maximum.
- At \(x=\tfrac{2}{3}\), \(y''=2>0\), so this is a local minimum.
The inflection point is where \(y''=0\): \[ 6x-2=0 \Rightarrow x=\tfrac{1}{3}. \]
Takeaway. First derivative = where the slope is zero. Second derivative = which way the curve bends. Together they classify maxima, minima, and inflection points.