EE 364A (Convex Optimization): Chapter 4.7 - Vector Optimization
Vector Optimization
Vector optimization (multiobjective optimization) replaces a scalar objective with a vector-valued objective. Because vector values are only partially ordered, a single global optimum often does not exist. This motivates Pareto optimality and scalarization.
General vector optimization problem
Let \(f_0: \mathbb{R}^n \to \mathbb{R}^q\) be the vector objective, with scalar constraints \(f_i(x) \le 0\) and equality constraints \(h_i(x)=0\): \[ \begin{aligned} \text{minimize (w.r.t. }K) &\quad f_0(x) \\ \text{subject to } &\quad f_i(x) \le 0,\quad i=1,\dots,m \\ &\quad h_i(x)=0,\quad i=1,\dots,p. \end{aligned} \] Here \(K \subseteq \mathbb{R}^q\) is a proper cone that defines the ordering. We interpret \[ f_0(x) \preceq_K f_0(y) \] as “\(x\) is no worse than \(y\)” with respect to \(K\) and the objective components.
Unlike scalar optimization, two objective vectors are often incomparable.
Achievable objective set and optimal points
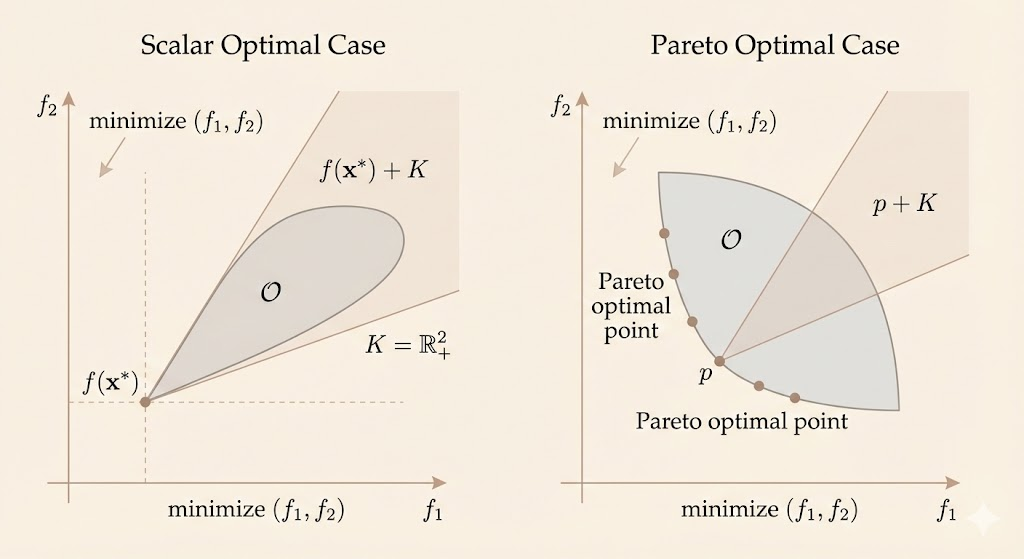
Define the set of achievable objective values \[ \mathcal{O} = \{ f_0(x) \mid x \in \mathcal{D},\ f_i(x)\le 0,\ h_i(x)=0 \} \subseteq \mathbb{R}^q. \] If \(\mathcal{O}\) has a minimum element (with respect to \(K\)), then an optimal point exists. A point \(x^*\) is optimal iff \[ \mathcal{O} \subseteq f_0(x^*) + K. \] In this case, every feasible objective value is dominated by \(f_0(x^*)\).
Pareto optimal points and values
Often \(\mathcal{O}\) has no minimum element. A feasible point \(x\) is Pareto optimal if there is no feasible point that improves all objectives simultaneously. Equivalently, \[ \big(f_0(x) - K\big) \cap \mathcal{O} = \{ f_0(x) \}. \] The set of Pareto optimal values is \[ \mathcal{P} \subseteq \mathcal{O} \cap \partial \mathcal{O}. \] Intuitively, Pareto points lie on the boundary of achievable values and represent efficient trade-offs.
Multicriterion optimization
What is multicriterion optimization?
A multicriterion (multiobjective) optimization problem seeks to optimize multiple scalar objectives at once: \[ F(x) = (F_1(x),\dots,F_q(x)), \] typically with the goal of minimizing all components.
Why introduce it?
In scalar optimization, feasible points are totally ordered. In multicriterion optimization: - Two feasible points can be incomparable. - A point can be better in some objectives and worse in others. - A single global optimum often does not exist.
This motivates Pareto optimality. A feasible point \(x^*\) is Pareto optimal if there is no feasible \(y\) such that \[ F_i(y) \le F_i(x^*)\ \forall i,\quad \text{with strict inequality for at least one } i. \] The Pareto set describes the efficient trade-off surface.
Relationship to scalarization
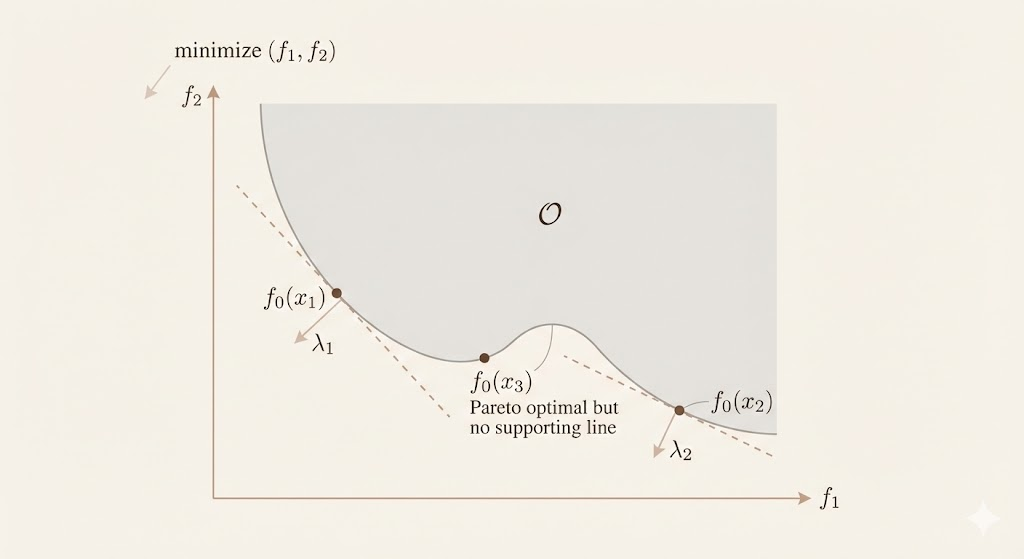
Scalarization converts the vector objective into a weighted sum by choosing weights: \[ \min_x \ \lambda^\top F(x),\quad \lambda \in K^*,\ \lambda \succ 0. \] Geometrically, each \(\\lambda\) defines a supporting hyperplane of the achievable set. The point of contact is Pareto optimal. However, Pareto points in non-convex regions of the boundary may not be recovered by any choice of weights.
A simple example
Consider \(f_0(x) = (x^2, (x-1)^2)\) with \(x \in \mathbb{R}\). Minimizing one component increases the other, so there is no single best \(x\). The Pareto set is the interval between the two minimizers, capturing the trade-off curve.
Scalarization
A standard method to recover Pareto points is scalarization. Choose \[ \lambda \succ_{K^*} 0, \] where \(K^*\) is the dual cone. Then solve the scalar problem \[ \begin{aligned} \text{minimize} &\quad \lambda^\top f_0(x) \\ \text{subject to } &\quad f_i(x) \le 0,\quad i=1,\dots,m \\ &\quad h_i(x)=0,\quad i=1,\dots,p. \end{aligned} \]
Key facts: - Every scalarized solution is Pareto optimal, but not every Pareto point is found by weights. - Geometrically, scalarization finds supporting hyperplanes of \(\mathcal{O}\) with normal \(\lambda\). - If \(\mathcal{O}\) is convex, all Pareto points on exposed faces are reachable by some \(\lambda\).
Why this matters
Vector optimization provides the language for trade-offs in real systems (cost vs. accuracy, risk vs. return, speed vs. energy). Pareto optimality describes what is truly efficient, and scalarization connects multiobjective structure to standard convex optimization tools.