Lecture 13: Randomized Matrix Multiplication
Randomized matrix multiplication replaces a full \(AB\) with a low-rank approximation built from sampled outer products. The key is to choose sampling probabilities that keep the estimator unbiased while minimizing variance.
Variance and mean
For outcomes \(o_i\) sampled with probabilities \(p_i\):
\[ \mu = \sum_i p_i o_i, \quad \sigma^2 = \sum_i p_i (o_i - \mu)^2. \]
For equally likely samples with \(p_i = 1/n\) this reduces to \[ \mu = \frac{1}{n}\sum_{i=1}^n o_i, \quad \sigma^2 = \frac{1}{n}\sum_{i=1}^n (o_i - \mu)^2. \]
A convenient form of the variance is \[ \begin{aligned} \sigma^2 &= \sum_i p_i (o_i - \mu)^2 \\ &= \sum_i p_i o_i^2 - 2\mu\sum_i p_i o_i + \mu^2\sum_i p_i \\ &= \sum_i p_i o_i^2 - \mu^2, \end{aligned} \] using \(\sum_i p_i = 1\) and \(\sum_i p_i o_i = \mu\).
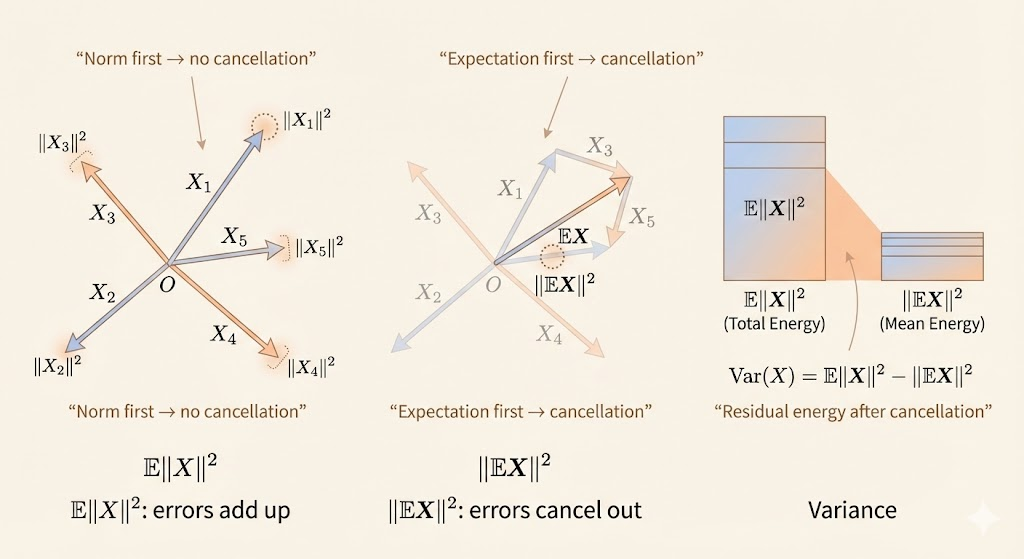
For a random vector \(X\) this becomes \[ \mathrm{Var}(X) = \mathbb{E}\|X\|^2 - \|\mathbb{E}X\|^2. \] Taking the norm before expectation destroys cancellation; taking the expectation first allows positive and negative errors to cancel.
Random selection for matrix products
Let \(A \in \mathbb{R}^{m\times r}\) and \(B \in \mathbb{R}^{r\times n}\). Write \[ AB = \sum_{j=1}^r a_j b_j^\top, \] where \(a_j\) is column \(j\) of \(A\) and \(b_j^\top\) is row \(j\) of \(B\).
We sample index \(j\) with probability \(p_j\) and form rank-1 outer products. A natural weight is \[ P_j = \|a_j\|\,\|b_j\|, \] so the normalized distribution is \[ C = \sum_{j=1}^r \|a_j\|\,\|b_j\|, \quad p_j = \frac{P_j}{C}. \]
With \(s\) samples, \[ \widetilde{AB} = \frac{1}{s}\sum_{t=1}^s \frac{a_{j_t} b_{j_t}^\top}{p_{j_t}}. \]
This estimator is unbiased: \[ \mathbb{E}[\widetilde{AB}] = AB. \]
Its variance (in Frobenius norm) is \[ \mathrm{Var}(\widetilde{AB}) = \frac{1}{s}\left(\sum_{j=1}^r \frac{\|a_j\|^2\,\|b_j\|^2}{p_j} - \|AB\|_F^2\right) = \frac{1}{s}\left(C^2 - \|AB\|_F^2\right). \]
Optimizing the sampling probabilities
We minimize the variance term by solving \[ \begin{aligned} \text{minimize} &\quad \sum_{j=1}^r \frac{\|a_j\|^2\,\|b_j\|^2}{p_j} \\ \text{subject to} &\quad \sum_{j=1}^r p_j = 1, \; p_j \ge 0. \end{aligned} \]
Introduce the Lagrangian \[ \mathcal{L}(p,\lambda)=\sum_{j=1}^r \frac{\|a_j\|^2\,\|b_j\|^2}{p_j}+\lambda\left(\sum_{j=1}^r p_j-1\right). \] Let \(w_j=\|a_j\|\,\|b_j\|\). Differentiating w.r.t. \(p_j\) gives \[ \frac{\partial \mathcal{L}}{\partial p_j}=-\frac{w_j^2}{p_j^2}+\lambda=0 \quad\Rightarrow\quad p_j=\frac{w_j}{\sqrt{\lambda}}. \] Differentiating w.r.t. \(\lambda\) enforces the constraint: \[ \frac{\partial \mathcal{L}}{\partial \lambda}=\sum_{j=1}^r p_j-1=0 \quad\Rightarrow\quad \sqrt{\lambda}=\sum_{j=1}^r w_j. \] Therefore \[ p_j^\star = \frac{w_j}{\sum_{k=1}^r w_k} = \frac{\|a_j\|\,\|b_j\|}{\sum_{k=1}^r \|a_k\|\,\|b_k\|}. \]
So we should sample column-row pairs proportional to the product of their norms.
Summary
Randomized matrix multiplication approximates \(AB\) by sampling rank-1 outer products. The estimator remains unbiased, and the optimal sampling rule is to pick indices proportional to \(\|a_j\|\,\|b_j\|\), which minimizes variance for a fixed sample size.