EE 364A (Convex Optimization): Chapter 4.4 - Quadratic Optimization Problems
Quadratic Optimization Problems (QP)
A convex optimization problem is a quadratic program (QP) if:
- the objective is convex quadratic
- the inequality constraints are affine
A standard form is \[ \begin{aligned} \text{minimize} &\quad \frac{1}{2}x^\top Px + q^\top x + r \\ \text{subject to} &\quad Gx \preceq h \\ &\quad Ax = b \end{aligned} \] where \(P \in S_+^n\), \(G \in \mathbb{R}^{m\times n}\), and \(A \in \mathbb{R}^{p\times n}\).
Examples
Least squares
\[ \text{minimize} \quad \|Ax-b\|_2^2 \] This unconstrained problem has the closed-form solution \(x = A^+ b\).
Adding simple box constraints turns it into a QP: \[ \begin{aligned} \text{minimize} &\quad \|Ax-b\|_2^2 \\ \text{subject to} &\quad l_i < x_i < u_i, \quad i=1,\dots,n \end{aligned} \]
Linear program with random cost
Start from the linear program \[ \begin{aligned} \text{minimize} &\quad c^\top x \\ \text{subject to} &\quad Gx \preceq h \\ &\quad Ax = b \end{aligned} \] Assume the cost is random with mean \(\bar{c}\) and covariance \(\Sigma\). A risk-averse formulation becomes the QP \[ \begin{aligned} \text{minimize} &\quad \bar{c}^\top x + \gamma x^\top \Sigma x = \mathbb{E}[c^\top x] + \gamma \mathrm{Var}(c^\top x) \\ \text{subject to} &\quad Gx \preceq h \\ &\quad Ax = b \end{aligned} \] where \(\gamma > 0\) is a risk-aversion parameter.
Quadratically Constrained Quadratic Programs (QCQP)
If the inequality constraints are also convex quadratics, the problem is a QCQP: \[ \begin{aligned} \text{minimize} &\quad \frac{1}{2}x^\top P_0 x + q_0^\top x + r_0 \\ \text{subject to} &\quad \frac{1}{2}x^\top P_i x + q_i^\top x + r_i \le 0, \quad i=1,\dots,m \\ &\quad Ax = b \end{aligned} \] Each \(P_i \succeq 0\) ensures convexity.
Second-Order Cone Programs (SOCP)
A second-order cone program has constraints of the form \[ \begin{aligned} \text{minimize} &\quad f^\top x \\ \text{subject to} &\quad \|A_i x + b_i\|_2 \le c_i^\top x + d_i, \quad i=1,\dots,m \\ &\quad Fx = g \end{aligned} \]
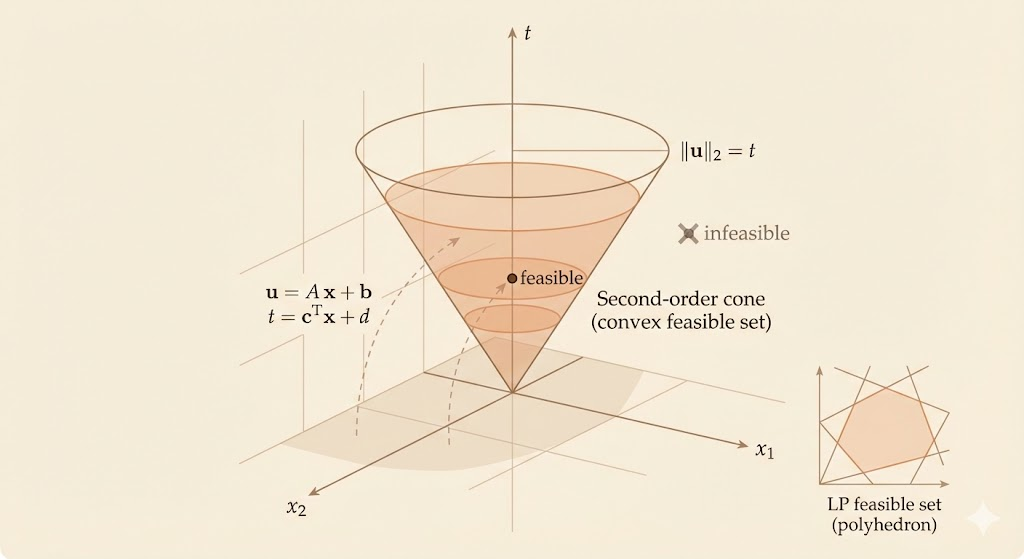
Special cases:
- If \(c_i = 0\) for all \(i\), the SOCP becomes a QCQP: \((A_i x + b_i)^\top (A_i x + b_i) \le d_i^2\).
- If \(A_i = 0\) for all \(i\), the SOCP becomes a linear program: \(-c_i^\top x - d_i \le -\|b_i\|\).
SOCPs unify QP and QCQP in a single convex framework.
Robust Linear Programming
In many applications, the parameters in the constraints are uncertain: \[ \begin{aligned} \text{minimize} &\quad c^\top x \\ \text{subject to} &\quad a_i^\top x \le b_i, \quad i=1,\dots,m \end{aligned} \]
Deterministic (ellipsoidal) model
Assume each uncertain vector lies in an ellipsoid \[ \mathcal{E}_i = \{\bar{a}_i + P_i u \mid \|u\|_2 \le 1\}. \] The robust constraint becomes \[ \bar{a}_i^\top x + \|P_i^\top x\|_2 \le b_i, \] which is an SOCP because \[ \sup_{\|u\|_2 \le 1} u^\top (P_i^\top x) = \|P_i^\top x\|_2. \]
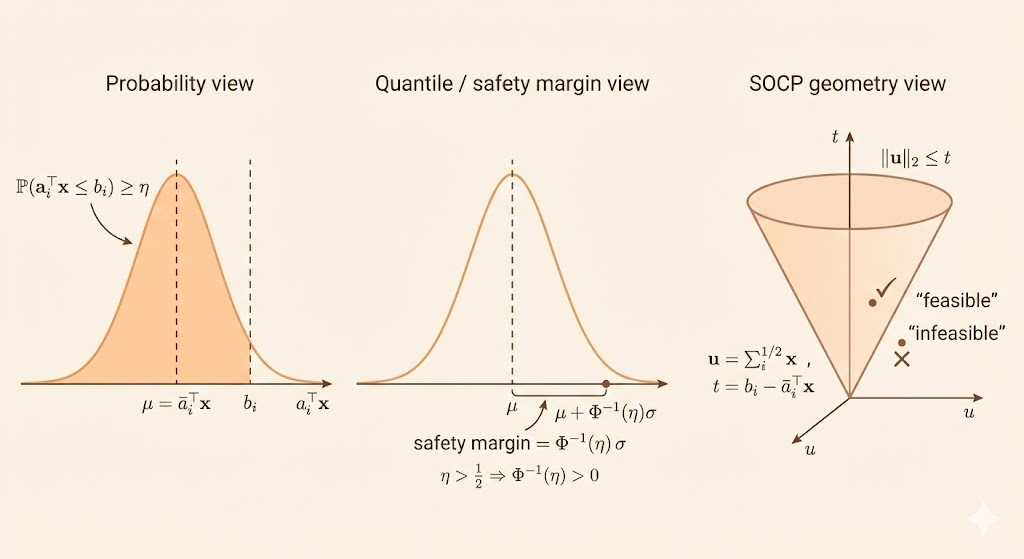
Stochastic (chance) model
Assume \(a_i \sim \mathcal{N}(\bar{a}_i, \Sigma_i)\). Then \(a_i^\top x\) is Gaussian with
- mean \(\bar{a}_i^\top x\)
- variance \(x^\top \Sigma_i x\)
A chance constraint \[ \mathrm{prob}(a_i^\top x \le b_i) \ge \eta \] reduces to the SOCP \[ \bar{a}_i^\top x + \Phi^{-1}(\eta)\|\Sigma_i^{1/2} x\|_2 \le b_i, \] for \(\eta \ge 1/2\).