EE 364A (Convex Optimization): Lecture 4.2 - Conjugate & Quasiconvex Functions
Conjugate Functions
The conjugate of a function \(f(x)\) is
\[ f^*(y) = \sup_{x \in \text{dom } f} (y^\top x - f(x)) \]
Key property: The conjugate function \(f^*(y)\) is always convex, even if \(f(x)\) is not convex.
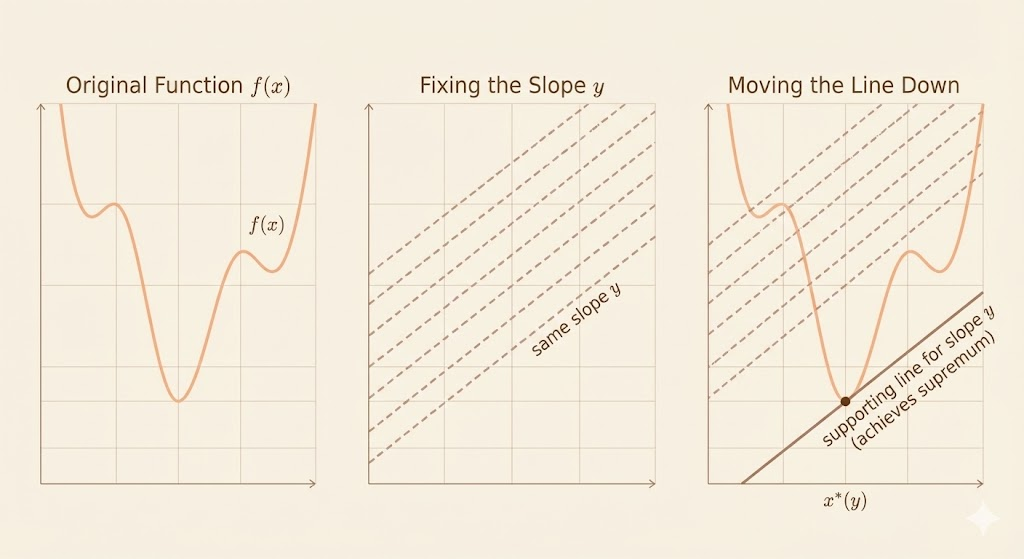
Examples
Example 1: Negative Logarithm
For \(f(x) = -\log(x)\):
\[ f^*(y) = \sup_{x > 0} (xy + \log x) = \begin{cases} -1 - \log(-y) & y < 0 \\ \infty & \text{otherwise} \end{cases} \]
Example 2: Strictly Convex Quadratic
For \(f(x) = \frac{1}{2}x^\top Q x\) with \(Q \in S_{++}^n\) (strictly positive definite):
\[ f^*(y) = \sup_{x} \left( y^\top x - \frac{1}{2}x^\top Q x \right) = \frac{1}{2}y^\top Q^{-1}y \]
The conjugate is also quadratic, with the inverse of the Hessian.
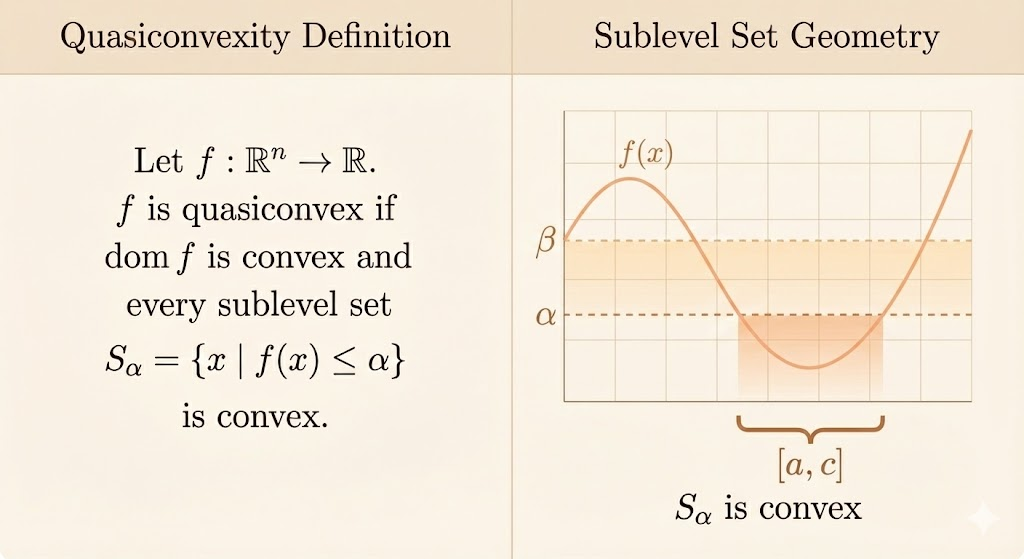
Quasiconvex Functions
A function \(f: \mathbb{R}^n \to \mathbb{R}\) is quasiconvex if:
- \(\text{dom } f\) is convex
- The sublevel sets are convex for all \(\alpha\):
\[ S_\alpha = \{x \in \text{dom } f \mid f(x) \leq \alpha\} \]
Related definitions: - \(f\) is quasiconcave if \(-f\) is quasiconvex - \(f\) is quasilinear if it is both quasiconvex and quasiconcave
Examples
\(\sqrt{|x|}\) is quasiconvex on \(\mathbb{R}\)
\(\text{ceil}(x) = \inf\{z \in \mathbb{Z} \mid z \geq x\}\) is quasilinear
\(\log(x)\) is quasilinear on \(\mathbb{R}_{++}\)
\(f(x_1, x_2) = x_1 x_2\) is quasiconcave on \(\mathbb{R}_{++}^2\)
Linear-fractional function: \[ f(x) = \frac{a^\top x + b}{c^\top x + d}, \quad \text{dom } f = \{x \mid c^\top x + d > 0\} \] is quasilinear
Distance ratio: \[ f(x) = \frac{\|x - a\|_2}{\|x - b\|_2}, \quad \text{dom } f = \{x \mid \|x - a\|_2 \leq \|x - b\|_2\} \] is quasiconvex
Modified Jensen Inequality
For quasiconvex functions, Jensen’s inequality becomes:
\[ f(\theta x + (1 - \theta)y) \leq \max\{f(x), f(y)\} \quad \text{for } 0 \leq \theta \leq 1 \]
This says that a quasiconvex function along a line segment is bounded by the maximum of the endpoint values, rather than a weighted average (as in the standard Jensen inequality for convex functions).