EE 364A (Convex Optimization): Lecture 5.1 - Log-Concave and Log-Convex Functions
Convex Optimization
Log-Concave
Log-Convex Functions
Convex Optimization Textbook - Chapter 3.5 (page 118)
Log-Concave and Log-Convex functions
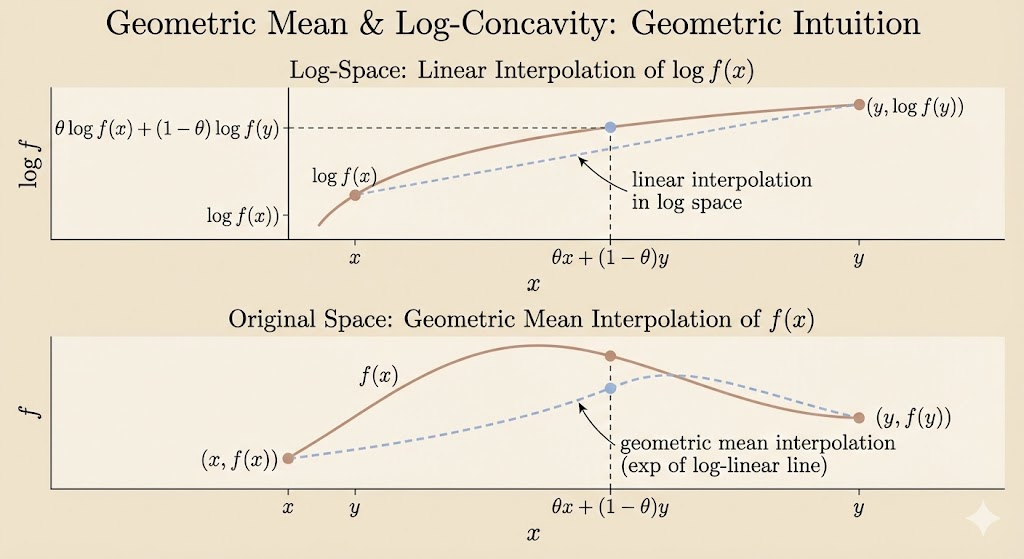
A positive function \(f\) is log-concave if \(\log f\) is concave:
\[ f(\theta x+(1-\theta)y)\ge f(x)^\theta f(y)^{1-\theta} \quad \text{for }0\le\theta\le 1 \]
\(f\) is log-convex if \(\log f\) is convex.
Proof
To prove: \[ \log(f(\theta x+(1-\theta)y))\ge \theta \log f(x)+(1-\theta)\log f(y) \]
Take exponential on both sides: \[ \begin{aligned} \exp(\log(f(\theta x+(1-\theta)y))) &\ge \exp(\theta \log f(x)+(1-\theta)\log f(y))\\ f(\theta x+(1-\theta)y) &\ge \exp(\theta \log f(x)) \cdot \exp((1-\theta)\log f(y))\\ &\ge f(x)^\theta \cdot f(y)^{1-\theta} \end{aligned} \]
Final inequality: \[ f(\theta x+(1-\theta)y)\ge f(x)^\theta\cdot f(y)^{1-\theta} \]
Examples
- Powers: \(x^a\) on \(\mathbb{R}_{++}\) is log-convex for \(a \le 0\), log-concave for \(a \ge 0\)
- \(f(x)=\log(x^a)=a\log(x)\)
- \(f'(x)=a\cdot \frac{1}{x}\)
- \(f''(x)=a\cdot -\frac{1}{x^2}\)
| Function \(f(x)\) | Domain | Second Derivative / Curvature | Convex / Concave | \(\log f(x)\) | Log-Convex / Log-Concave | Key Notes |
|---|---|---|---|---|---|---|
| \(x^a\) | \(\mathbb{R}_{++}\) | \(a(a-1)x^{a-2}\) | depends on \(a\) | \(a\log x\) | \(a\ge 0\): log-concave \(a\le 0\): log-convex |
Classic Boyd example |
| \(e^{ax}\) | \(\mathbb{R}\) | \(a^2 e^{ax}\) | convex (all \(a\)) | \(ax\) | both | Exponential is always convex |
| \(\log x\) | \(\mathbb{R}_{++}\) | \(-1/x^2\) | concave | \(\log\log x\) | — | Fundamental concave function |
| Gaussian pdf \(\phi(x)\) | \(\mathbb{R}\) | — | ❌ | \(-x^2/2 + c\) | log-concave | Core likelihood model |
| Gaussian CDF \(\Phi(x)\) | \(\mathbb{R}\) | \(-x\phi(x)\) | ❌ (S-shaped) | \(\log\Phi(x)\) | log-concave | Probit models |
| Logistic \(\sigma(x)\) | \(\mathbb{R}\) | changes sign | ❌ | concave | log-concave | Logistic regression |
| \(\\|x\\|_2\) | \(\mathbb{R}^n\) | — | convex | — | — | All norms are convex |
| \(\log\sum_i e^{x_i}\) | \(\mathbb{R}^n\) | Hessian \(\succeq 0\) | convex | — | — | Softmax / log-partition |
| \(\prod_i x_i\) | \(\mathbb{R}_{++}^n\) | — | ❌ | \(\sum_i \log x_i\) | log-concave | Geometric programming |
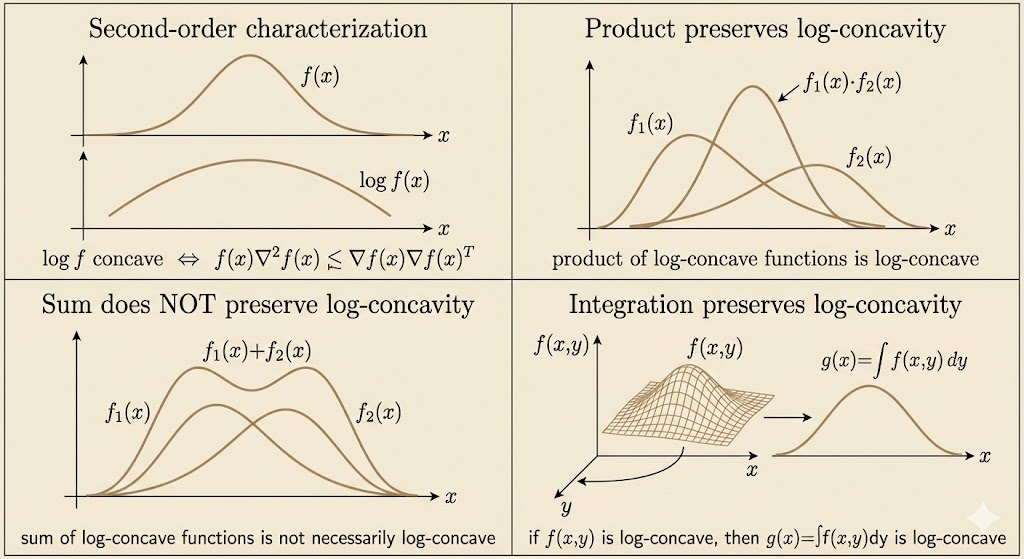
Properties of log-concave functions
- Twice differentiable function \(f\) with convex domain is log-concave iff \(f(x)\nabla^2f(x) \preceq \nabla f(x)\nabla f(x)^\top\) for all \(x \in \mathrm{dom}\, f\)
- Product of log-concave functions is log-concave
- Sum of log-concave functions is not always log-concave
- If \(f : \mathbb{R}^n \to \mathbb{R}\) is log-concave, then \(g(x)=\int f(x,y) dy\) is log-concave