Lecture 3: Convex Functions

Convex Optimization
Convex Functions
Optimization
Author

Chao Ma

Published

December 6, 2025

Separating Hyperplane Theorem

If C and D are nonempty disjoint convex sets, then there exists \(a \neq 0, b\) such that:

\[ a^\top x \leq b \quad \text{for } x \in C, \quad a^\top x \geq b \quad \text{for } x \in D \]

The hyperplane \(a^\top x = b\) separates C and D.

Separating hyperplane between two convex sets

Supporting Hyperplane Theorem

Supporting hyperplane to set C (doesn’t have to be a convex set) at boundary point \(x_0\):

\[ \{x \mid a^\top x = a^\top x_0\} \]

where \(a\) is the normal vector that determines the hyperplane tangent to C at point \(x_0\), with \(a \neq 0\) and \(a^\top x \leq a^\top x_0\) for \(x \in C\).

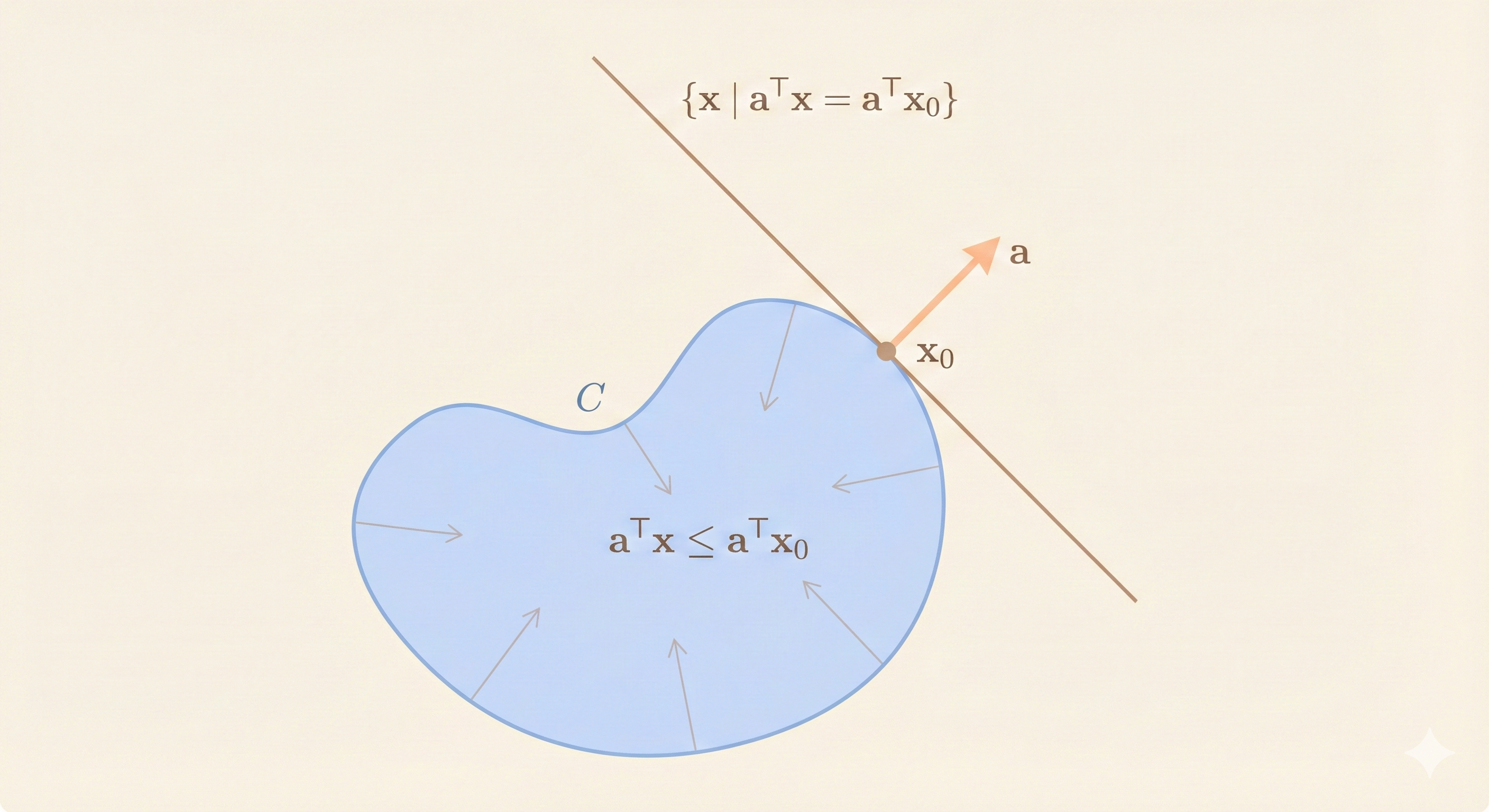
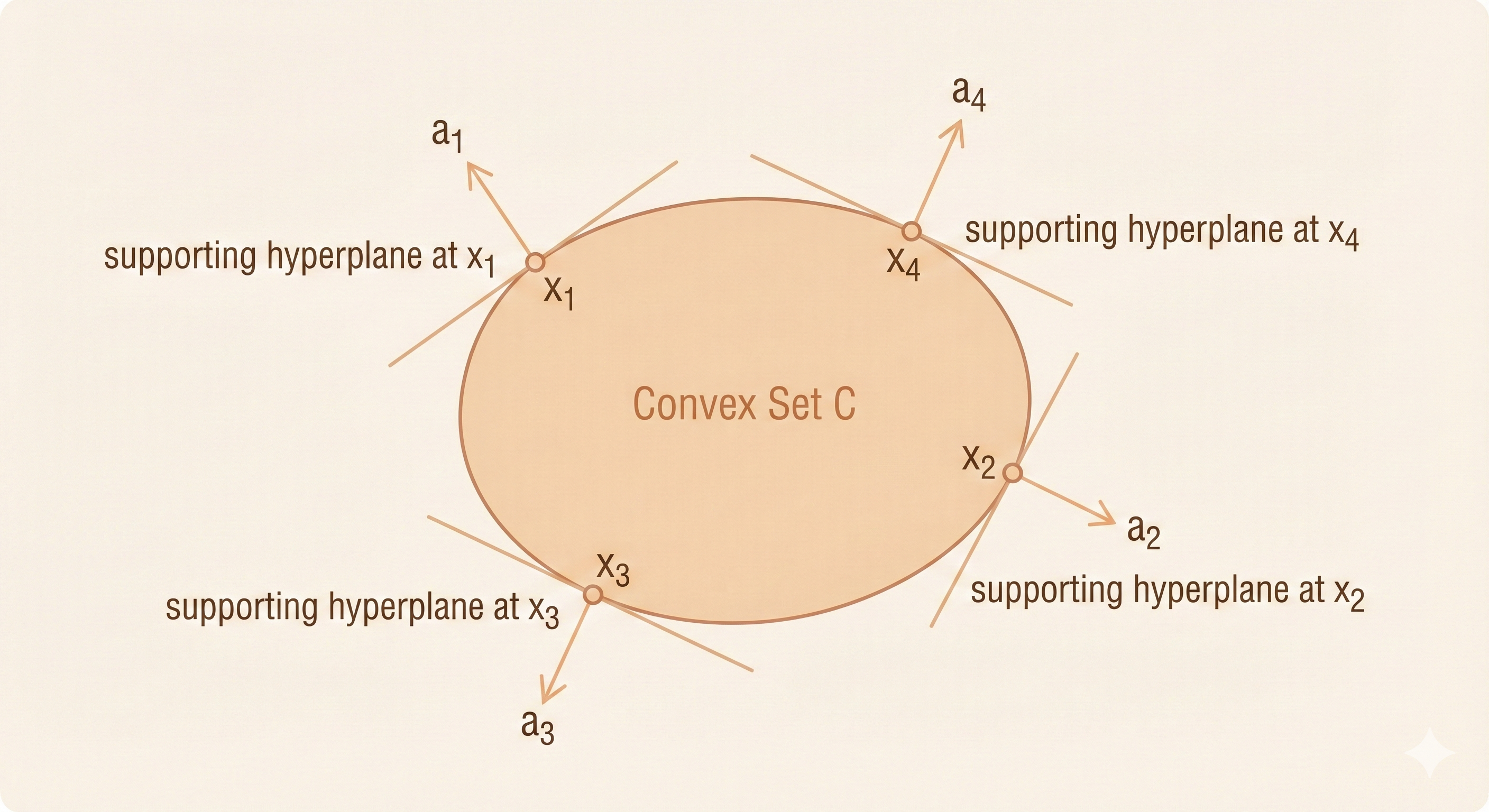
Supporting hyperplane at boundary point

If C is convex, then there is a supporting hyperplane at every point of its boundary.

Supporting hyperplanes exist at every boundary point for convex sets

Dual Cones and Generalized Inequalities

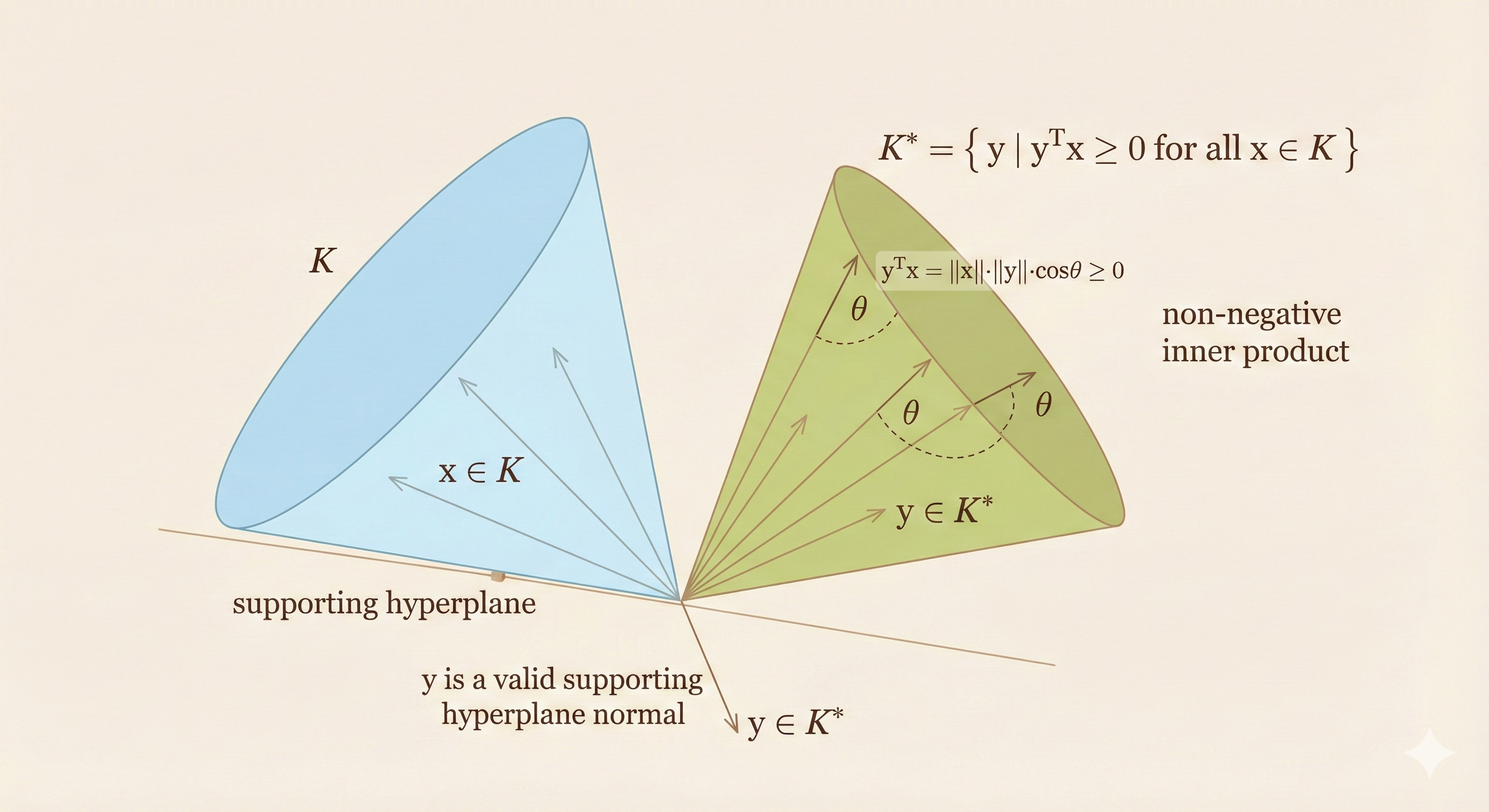
Dual cone of a cone K:

\[ K^* = \{y \mid y^\top x \geq 0 \quad \forall x \in K\} \]

The inner product of any vector in \(K^*\) and K is nonnegative.

Dual cone visualization

Examples

  • \(K = \{0\}\): the dual cone is \(K^* = \mathbb{R}^n\)
  • K is a ray: the dual cone is a half space
  • Self-dual cones:
    • \(K = \mathbb{R}_+^n\): dual cone \(K^* = K\)
    • \(K = S_+^n\) (positive semidefinite cone)
    • \(K = \{(x,t) \mid \|x\|_2 \leq t\}\) (second-order cone)
  • \(K = \{(x,t) \mid \|x\|_\infty \leq t\}\): dual cone \(K^* = \{(y,\tau) \mid \|y\|_1 \leq \tau\}\)

The dual cone of a proper cone is proper.

Minimum and Minimal Elements via Dual Inequalities

Minimum Element

\(x\) is the minimum element of S if and only if for all \(\lambda \succ_{K^*} 0\), \(x\) is the unique minimizer of \(\lambda^\top z\) over S.

Minimal Element

If \(x\) minimizes \(\lambda^\top z\) over S for some \(\lambda \succ_{K^*} 0\), then \(x\) is minimal.

If \(x\) is a minimal element of a convex set S, then there exists a nonzero \(\lambda \succ_{K^*} 0\) such that \(x\) minimizes \(\lambda^\top z\) over S.

Convex Functions

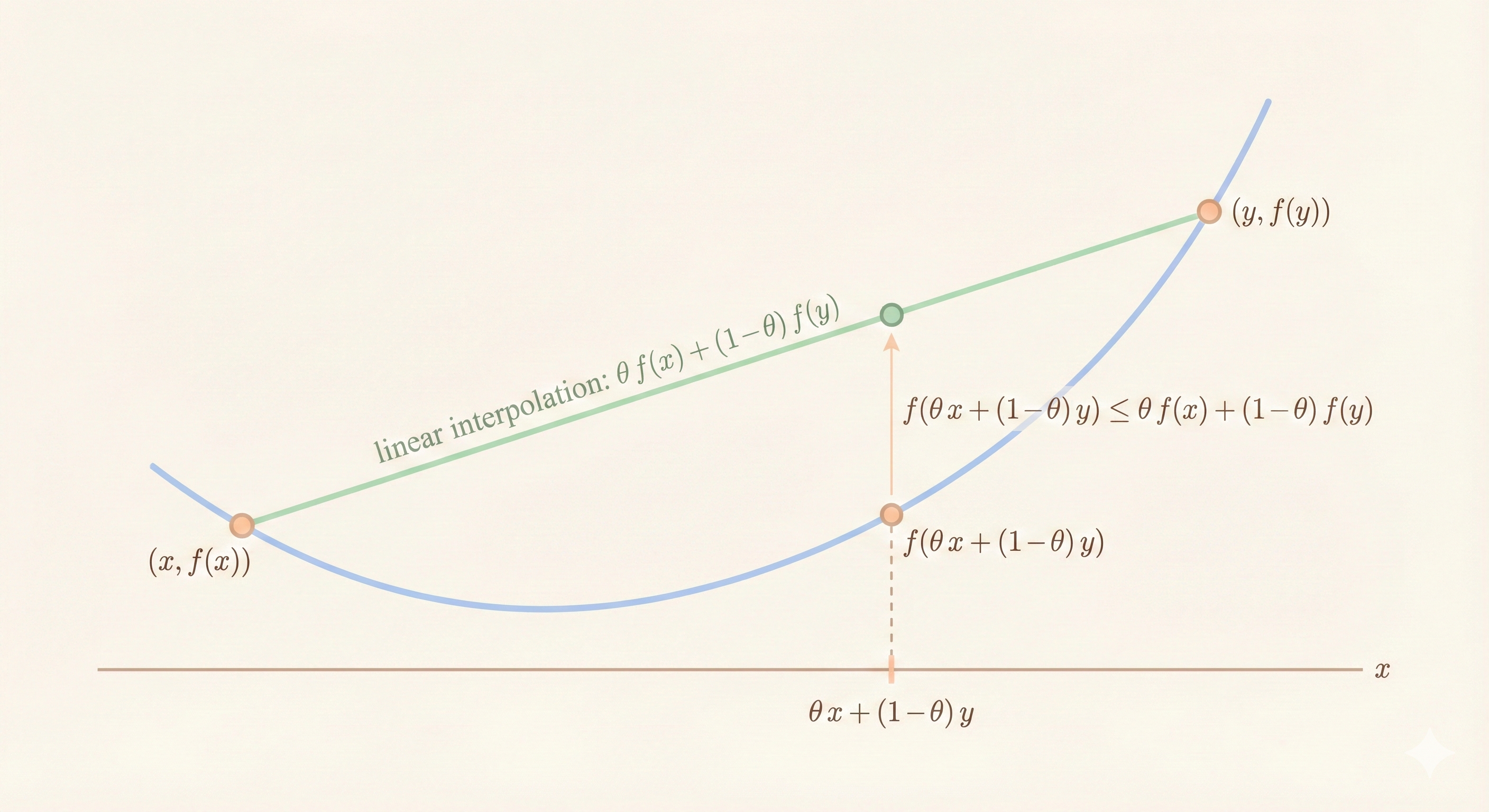
\(f: \mathbb{R}^n \rightarrow \mathbb{R}\) is convex if \(\text{dom } f\) is a convex set and:

\[ f(\theta x_1 + (1-\theta)x_2) \leq \theta f(x_1) + (1-\theta)f(x_2) \]

for all \(x_1, x_2 \in \text{dom } f\) and \(0 \leq \theta \leq 1\).

Convex function definition
  • \(f\) is concave if \(-f\) is convex
  • \(f\) is strictly convex if \(\text{dom } f\) is convex and: \[ f(\theta x_1 + (1-\theta)x_2) < \theta f(x_1) + (1-\theta)f(x_2) \] for all \(x_1, x_2 \in \text{dom } f\), \(x_1 \neq x_2\), and \(0 < \theta < 1\)

Examples on \(\mathbb{R}\)

Convex:

  • Affine: \(ax + b\) for any \(a, b \in \mathbb{R}\)
  • Exponential: \(e^{ax}\) for any \(a \in \mathbb{R}\)
  • Powers: \(x^a\) on \(\mathbb{R}_{++}\) for \(a \geq 1\) or \(a \leq 0\)
  • Powers of absolute value: \(|x|^p\) on \(\mathbb{R}\) for \(p \geq 1\)
  • Negative entropy: \(x \log x\) on \(\mathbb{R}_{++}\)

Concave:

  • Affine: \(ax + b\)
  • Powers: \(x^a\) on \(\mathbb{R}_{++}\) for \(0 \leq a \leq 1\)
  • Logarithm: \(\log x\) on \(\mathbb{R}_{++}\)

Examples on \(\mathbb{R}^n\) and \(\mathbb{R}^{m \times n}\)

On \(\mathbb{R}^n\):

  • Affine function: \(a^\top x + b\)
  • Norms: \(\|x\|_p = \sqrt[p]{\sum_i |x_i|^p}\); \(\|x\|_\infty = \max_k |x_k|\)

On \(\mathbb{R}^{m \times n}\):

  • Affine function: \(f(X) = \text{tr}(A^\top X) + b = \sum_{i,j} A_{ij} X_{ij} + b\)
  • Spectral norm: \(f(X) = \|X\|_2 = \sigma_{\max}(X)\)

Restriction of a Convex Function to a Line

\(f: \mathbb{R}^n \rightarrow \mathbb{R}\) is convex if and only if the function \(g: \mathbb{R} \rightarrow \mathbb{R}\):

\[ g(t) = f(x + tv), \quad \text{dom } g = \{t \mid x + tv \in \text{dom } f\} \]

is convex for any \(x \in \text{dom } f\), \(v \in \mathbb{R}^n\).

This allows checking convexity of \(f\) by checking convexity of functions of one variable.

Example

\(f: S^n \rightarrow \mathbb{R}\) with \(f(X) = \log \det X\), \(\text{dom } f = S_{++}^n\)

\[ g(t) = \log \det(X + tV) = \log \det X + \log \det(I + tX^{-1/2}VX^{-1/2}) = \log \det X + \sum_{i=1}^n \log(1 + t\lambda_i) \]

where \(\lambda_i\) are the eigenvalues of \(X^{-1/2}VX^{-1/2}\). Since \(g\) is concave, \(f\) is concave.

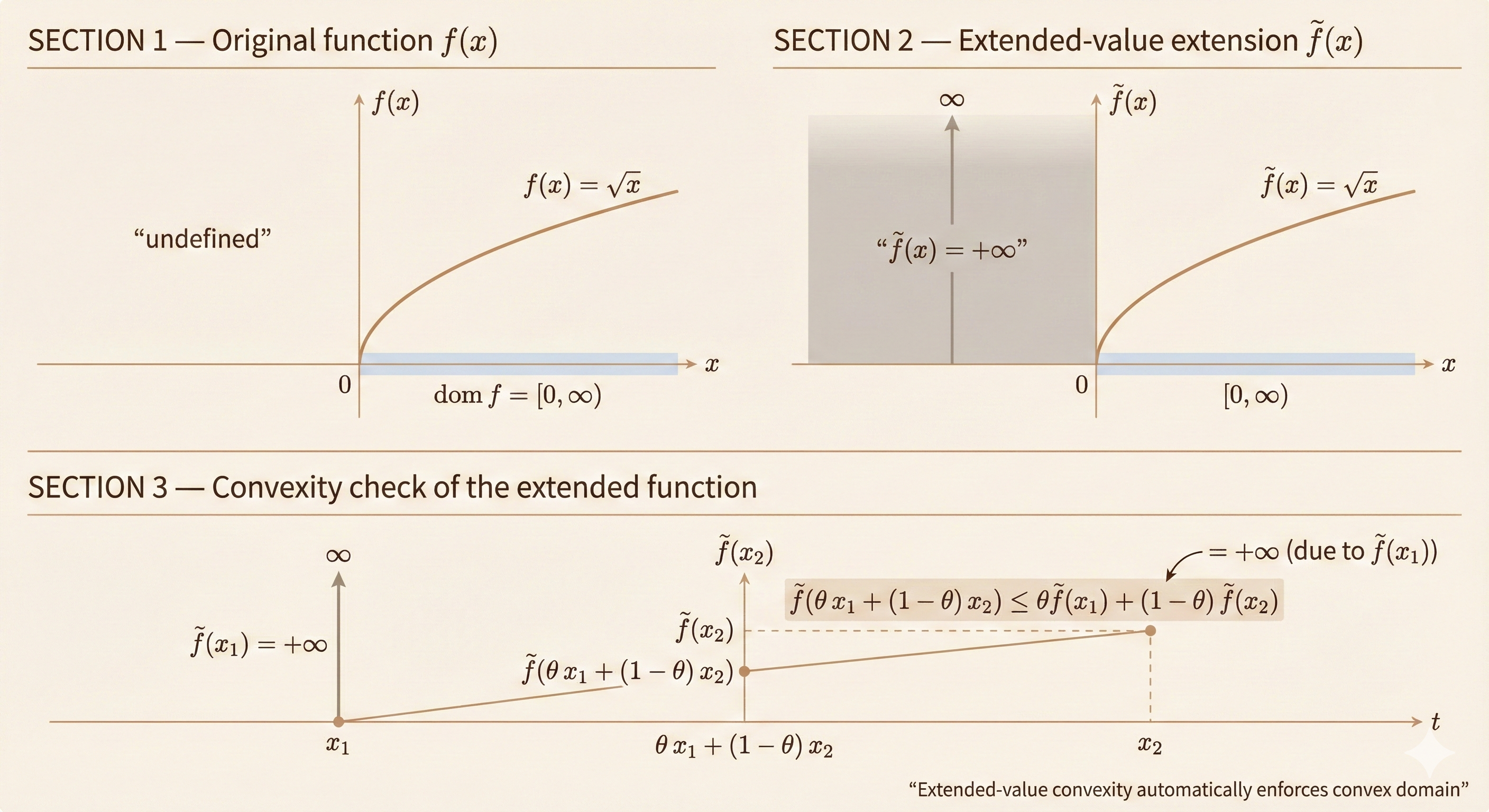
Extended Value Extension

\[ \tilde{f}(x) = \begin{cases} f(x) & x \in \text{dom } f \\ +\infty & x \notin \text{dom } f \end{cases} \]

This extends the output domain of \(f\) to \(\mathbb{R} \cup \{+\infty\}\).

Convexity of \(\tilde{f}(\theta x + (1-\theta)y) \leq \theta \tilde{f}(x) + (1-\theta)\tilde{f}(y)\) still holds because:

  • For \(x, y \in \text{dom } f\): \(f(x)\) is convex, and \(\theta x + (1-\theta)y \in \text{dom } f\) (domain of convex function is convex)
  • For \(x \notin \text{dom } f\) or \(y \notin \text{dom } f\): \(\tilde{f}(\theta x + (1-\theta)y) \leq +\infty\)

Extended value extension

First-Order Condition

\(f\) is differentiable if \(\text{dom } f\) is open and the gradient exists at each \(x \in \text{dom } f\):

\[ \nabla f(x) = \left(\frac{\partial f(x)}{\partial x_1}, \frac{\partial f(x)}{\partial x_2}, \ldots, \frac{\partial f(x)}{\partial x_n}\right) \]

First-order condition: Differentiable \(f\) with convex domain is convex if and only if:

\[ f(y) \geq f(x) + \nabla f(x)^\top (y - x) \quad \forall x, y \in \text{dom } f \]

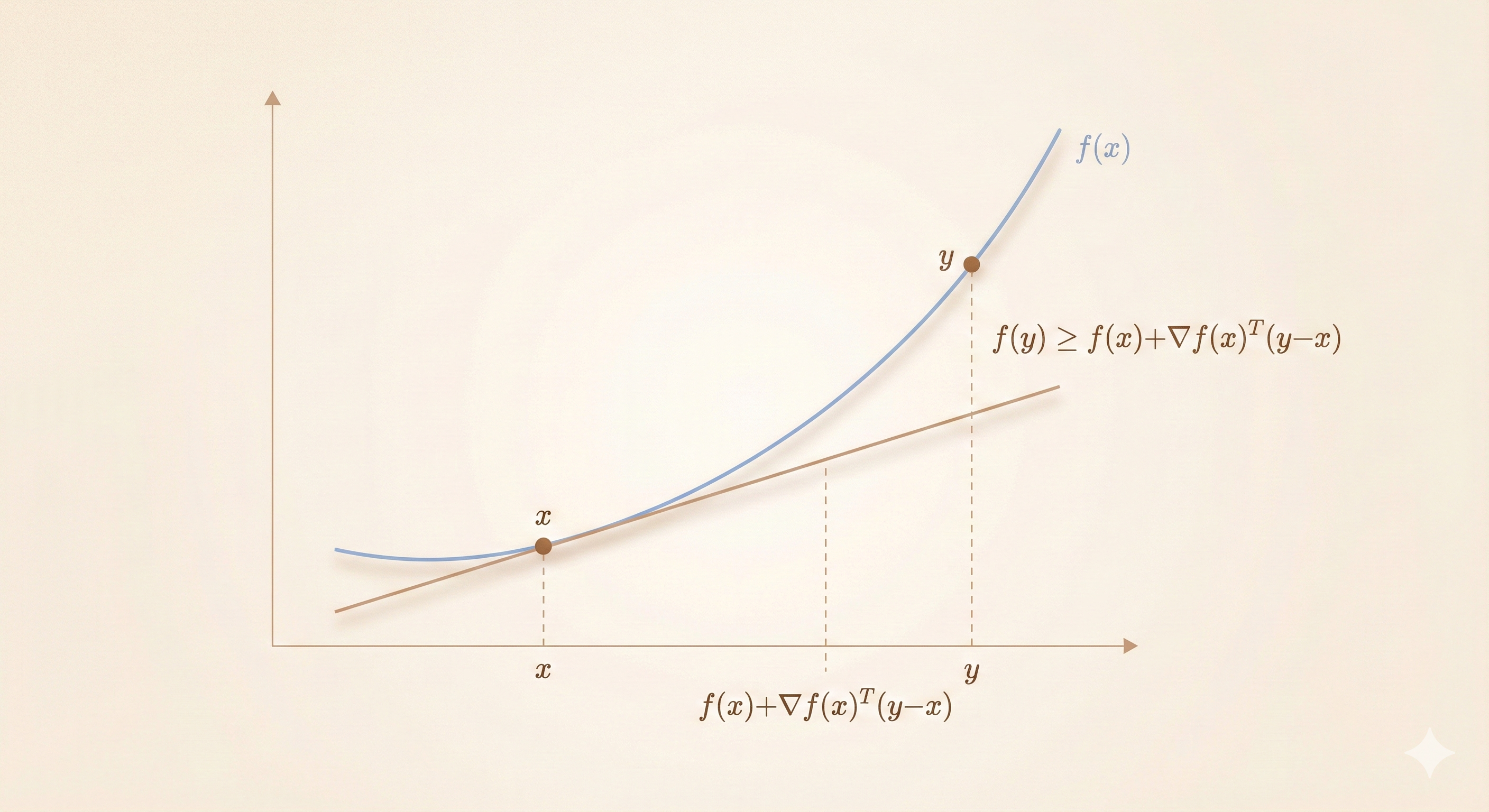
First-order condition: tangent always underestimates

Key insight: For a convex function, the tangent (first-order linear approximation) always underestimates the function.

Second-Order Conditions

\(f\) is twice differentiable if \(\text{dom } f\) is open and the Hessian \(\nabla^2 f(x) \in S^n\) exists at each \(x \in \text{dom } f\):

\[ \nabla^2 f(x)_{ij} = \frac{\partial^2 f(x)}{\partial x_i \partial x_j}, \quad i, j = 1, \ldots, n \]

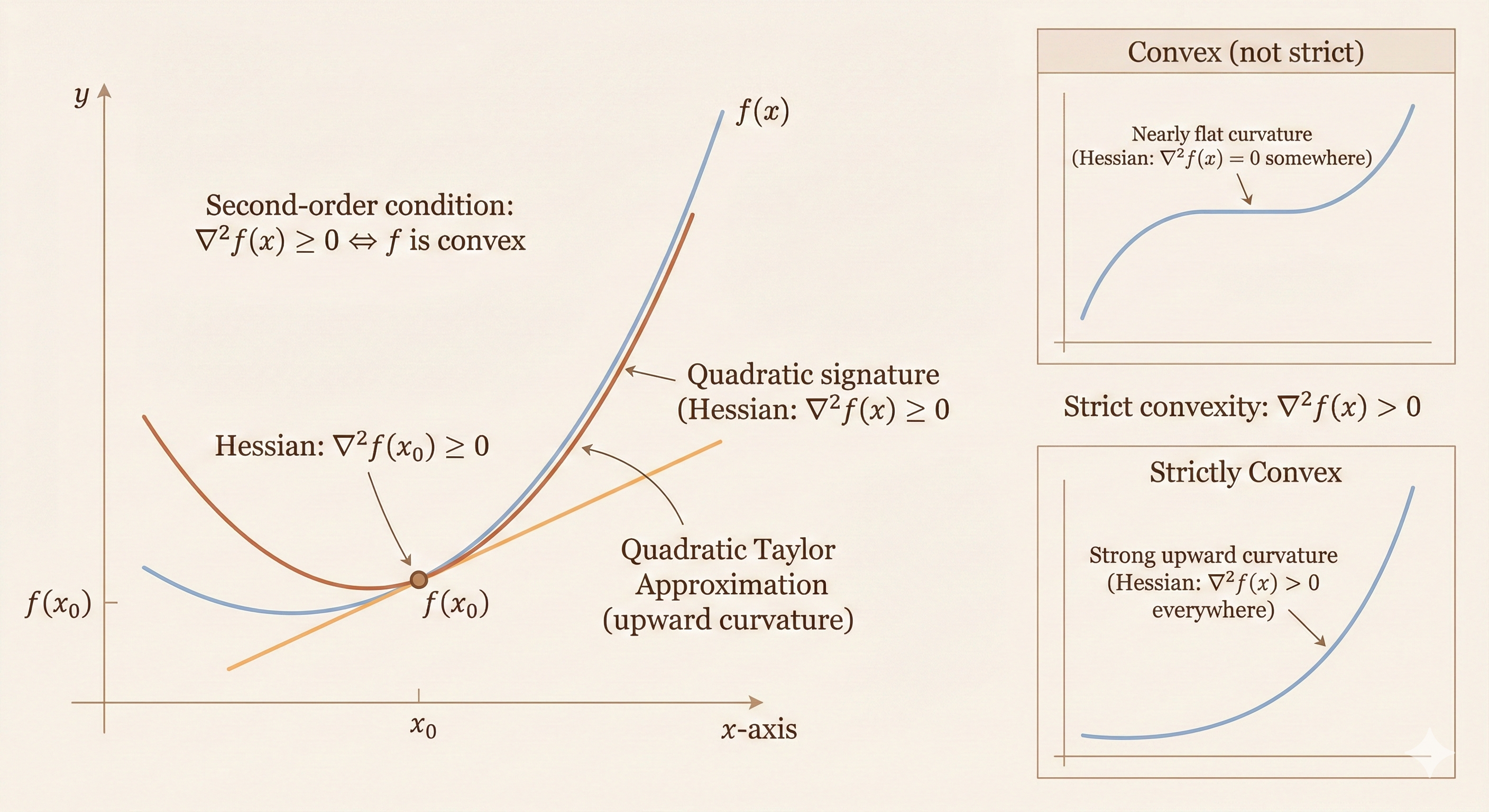
Second-order conditions: For twice differentiable \(f\) with convex domain:

  • \(f\) is convex if and only if \(\nabla^2 f(x) \succeq 0\) for all \(x \in \text{dom } f\)
  • If \(\nabla^2 f(x) \succ 0\), then \(f\) is strictly convex

Second-order condition visualization

Examples

Quadratic function: \(f(x) = \frac{1}{2}x^\top P x + q^\top x + r\) (with \(P \in S^n\))

\[ \nabla f(x) = Px + q, \quad \nabla^2 f(x) = P \]

If \(P \succeq 0\), then \(f(x)\) is convex.

Least-squares objective: \(f(x) = \|Ax - b\|_2^2\)

\[ \nabla f(x) = 2A^\top(Ax - b), \quad \nabla^2 f(x) = 2A^\top A \]

Convex for any \(A\), because \(A^\top A\) is always positive semidefinite.

Quadratic-over-linear: \(f(x, y) = x^2/y\) is convex if \(y > 0\)

\[ \nabla^2 f(x, y) = \frac{2}{y^3} \begin{bmatrix} y \\ -x \end{bmatrix} \begin{bmatrix} y & -x \end{bmatrix} \succeq 0 \]

Log-sum-exp: \(f(x) = \log \sum_{k=1}^n \exp x_k\) is convex

Let \(T = \sum_{k=1}^n \exp x_k\) and \(z_k = \exp x_k\):

\[ H = \nabla^2 f(x) = \frac{1}{T}\text{diag}(z) - \frac{1}{T^2}zz^\top \]

To verify H is PSD, check \(v^\top H v \geq 0\) for all \(v\):

\[ v^\top \nabla^2 f(x) v = \frac{\sum_k z_k v_k^2}{\sum_k z_k} - \frac{(\sum_k v_k z_k)^2}{(\sum_k z_k)^2} \]

By Cauchy-Schwarz inequality: \((\sum_k v_k z_k)^2 \leq (\sum_k z_k v_k^2)(\sum_k z_k)\), so \(v^\top \nabla^2 f(x) v \geq 0\).

Geometric mean: \(f(x) = \sqrt[n]{\prod_{k=1}^n x_k}\) on \(\mathbb{R}_{++}^n\) is concave.

Epigraph and Sub-level Sets

Sub-level Sets

\(\alpha\)-sublevel set of \(f: \mathbb{R}^n \rightarrow \mathbb{R}\):

\[ C_\alpha = \{x \in \text{dom } f \mid f(x) \leq \alpha\} \]

Sub-level sets of convex functions are convex (converse is false).

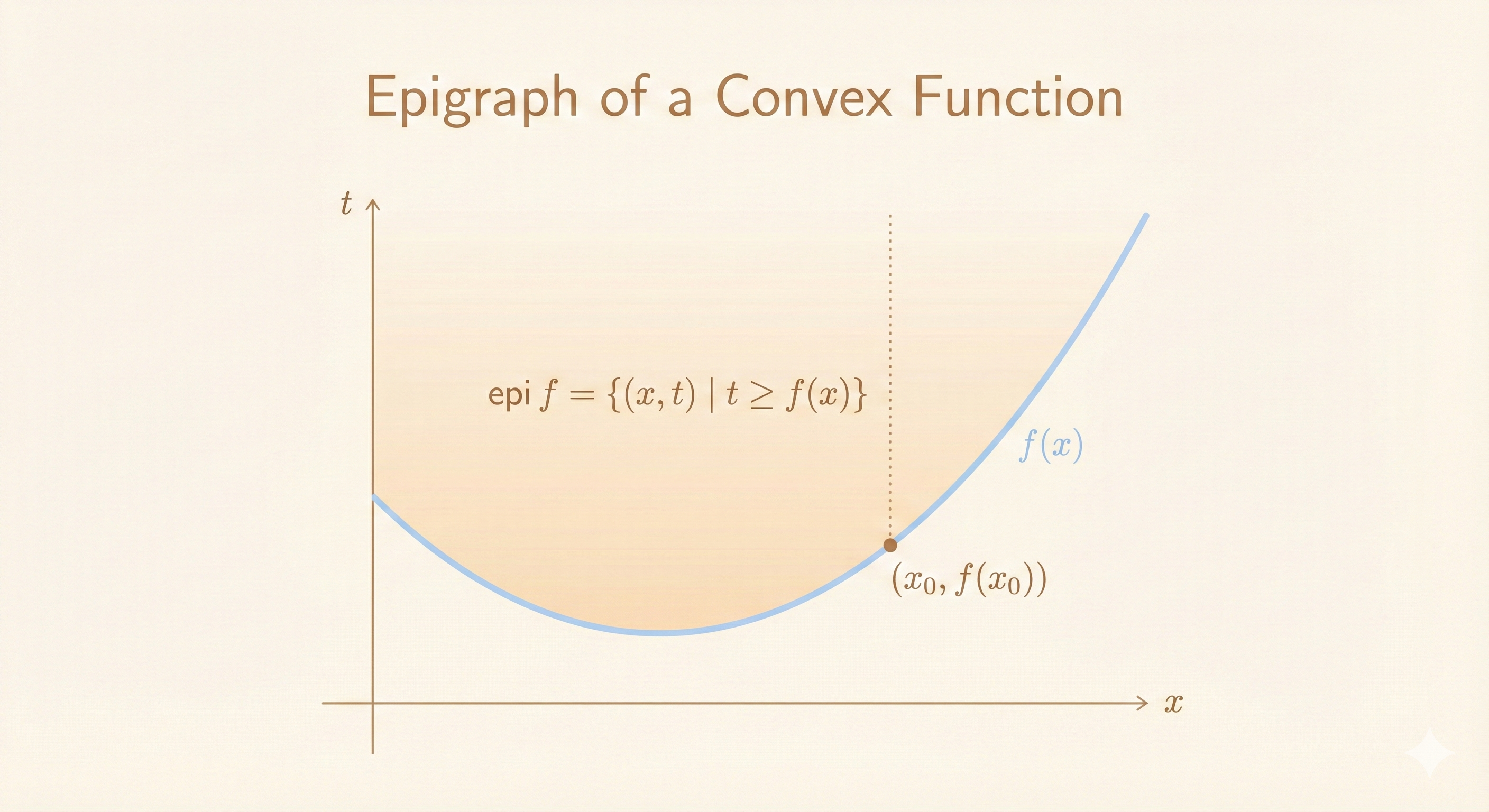
Epigraph

Epigraph of \(f: \mathbb{R}^n \rightarrow \mathbb{R}\):

\[ \text{epi } f = \{(x, t) \in \mathbb{R}^{n+1} \mid f(x) \leq t, \; x \in \text{dom } f\} \]

\(f\) is convex if and only if \(\text{epi } f\) is a convex set.

Epigraph of a convex function

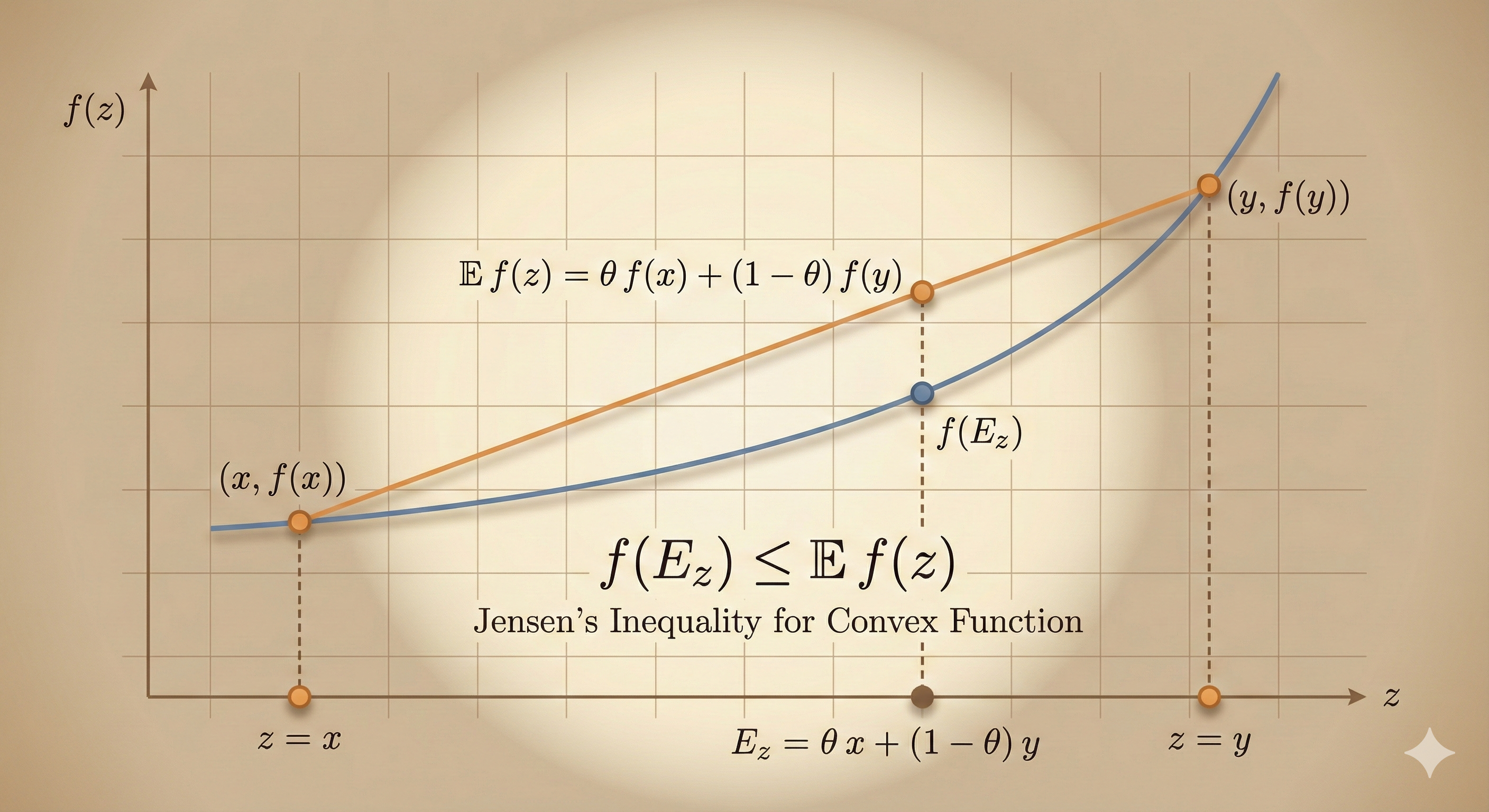
Jensen’s Inequality

If \(f\) is convex:

\[ f(\mathbb{E}[z]) \leq \mathbb{E}[f(z)] \]

for any random variable \(z\).

The function of the expectation is less than or equal to the expectation of the function.

The basic convexity inequality is a special case with discrete distribution:

  • \(\text{prob}(z = x) = \theta\)
  • \(\text{prob}(z = y) = 1 - \theta\)

Jensen’s inequality visualization

Operations that Preserve Convexity

Ways to establish convexity:

  1. Verify definition directly
  2. For twice differentiable functions, show \(\nabla^2 f(x) \succeq 0\)
  3. Combine simple convex functions using operations that preserve convexity:

Nonnegative weighted sum: \(f_1 + f_2\) is convex if \(f_1, f_2\) are convex

Nonnegative multiplication: \(\alpha f\) is convex if \(f\) is convex and \(\alpha > 0\)

Composition with affine function: \(f(Ax + b)\) is convex if \(f\) is convex

Pointwise maximum and supremum

Composition

Minimization

Perspective

Examples

Log barrier for linear inequalities: \[ f(x) = -\sum_{i=1}^m \log(b_i - a_i^\top x), \quad \text{dom } f = \{x \mid a_i^\top x < b_i, \; i = 1, \ldots, m\} \]

Norm of affine function: \[ f(x) = \|Ax + b\| \]

Key Insights

Convex functions are fundamental to optimization. The first-order condition shows that local information (gradient) provides a global lower bound. The second-order condition connects convexity to positive semidefiniteness of the Hessian. Jensen’s inequality generalizes the basic convexity definition to expectations, with applications throughout probability and machine learning. Operations preserving convexity allow building complex convex functions from simpler ones.