Goodfellow Deep Learning — Chapter 10.11: Optimizing Long-Term Dependencies
Deep Learning Book - Chapter 10.11 (page 408)
Gradient Clipping
Highly non-linear functions tend to produce gradients that are very large or very small.
Gradient cliff (gradient explosion cliff) refers to a loss landscape where large, relatively flat regions are separated by very steep walls. Near the current parameters, the gradient points toward the locally steepest descent, but a small step can suddenly cross into a region with much higher loss, because the surface rises sharply outside this narrow neighborhood.
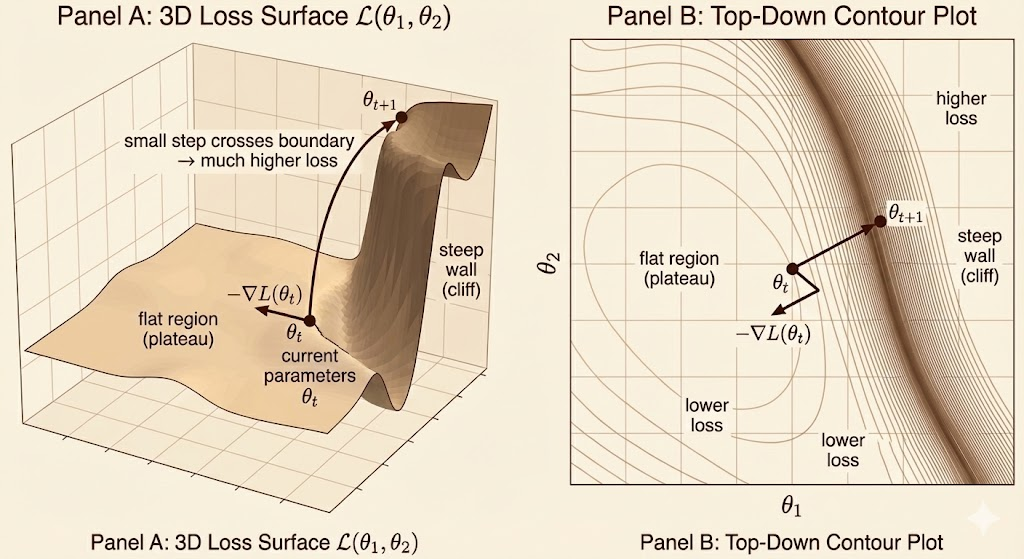
The Solution
\[ \text{if} \quad ||g|| > v\\ g \leftarrow \frac{gv}{||g||} \]
Gradient clipping rescales the gradient when its norm exceeds a threshold, ensuring that each parameter update remains bounded while preserving the descent direction. It prevents a single update from jumping across steep “gradient cliffs,” thereby stabilizing training in highly nonlinear models such as RNNs.
Regularizing Information Flow
We hope \(\left\|\frac{\partial h^t}{\partial h^{t-1}}\right\| \approx 1\). To achieve this, the following regularization term has been proposed:
\[ \Omega=\sum_t\left(\frac{\left\|(\nabla_{h^t} L)\frac{\partial h^t}{\partial h^{t-1}}\right\|}{\left\|\nabla_{h^t} L\right\|}-1\right)^2 \]
This regularization term is computationally expensive and difficult to implement, so it is rarely used in practice and mainly serves as a theoretical tool to understand gradient flow in recurrent networks.