Lecture 3: Orthonormal Columns
Orthonormal Matrices
- Two vectors are orthogonal if their inner product is 0: \(v_1^\top v_2=0\)
- A vector is a unit vector if its length is 1: \(||v||=1\)
- A matrix is orthogonal if its columns (equivalently, its rows) are orthonormal vectors
- \(Q^\top Q=QQ^\top =I\)
- An orthogonal matrix must be square, otherwise it is not invertible, so we can’t get \(QQ^\top=I\)
Example:
\[ A=\begin{bmatrix}1&0\\0&1\\0&0\end{bmatrix} \]
\[ A^\top A=\begin{bmatrix}1&0\\0&1\end{bmatrix} \]
\[ AA^\top=\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}\ne I \]
There are several important orthogonal matrices that arise naturally in real-world applications.
Rotation Matrix
A rotation matrix preserves the length of a vector; it only rotates the vector by some angle.
For example, \(\begin{bmatrix}\cos \theta& -\sin \theta \\ \sin \theta& \cos \theta\end{bmatrix}\), for any vector \([x_1,x_2]\), it changes the vector to \([\cos \theta x_1-\sin \theta x_2,\sin \theta x_1+\cos \theta x_2]\):
Length is preserved: \[(\cos \theta x_1-\sin \theta x_2)^2+(\sin \theta x_1+\cos \theta x_2)^2=(\cos^2 \theta+\sin^2 \theta)x_1^2+(\cos^2 \theta+ \sin^2 \theta)x_2^2=x_1^2+x_2^2\]
Dot product with original: \[[\cos \theta x_1-\sin \theta x_2,\sin \theta x_1+\cos \theta x_2]^\top\cdot [x_1,x_2]=\cos \theta (x_1^2+x_2^2)\]

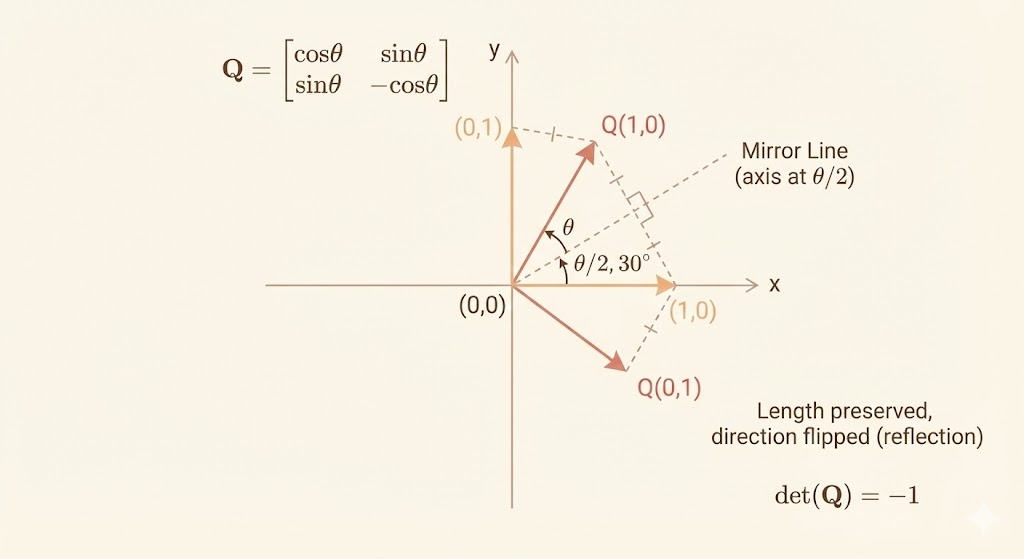
Reflection Matrix
A reflection matrix reflects vectors across a line (in 2D) or a plane (in 3D) while preserving their length.
\[ Q = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \]
It changes \([x_1,x_2] \to [x_1,-x_2]\)
General reflection across a line at angle \(\theta/2\):
\[ Q=\begin{bmatrix}\cos \theta &\sin\theta \\\sin\theta &-\cos\theta\end{bmatrix} \]
Householder Reflection
A Householder reflection is an orthogonal matrix of the form \(H = I - 2uu^\top\) that reflects vectors across the hyperplane orthogonal to \(u\).
Starting with \(u^\top u=1\) (unit vector \(u\)):
\[ H=I-2uu^\top \]
Properties: - \(H\) is symmetric, because \(I\) and \(uu^\top\) are both symmetric - \(H\) is orthogonal: \[ (I-2uu^\top)^\top(I-2uu^\top)=I-4uu^\top+4uu^\top uu^\top=I \]
Hadamard Matrices
A Hadamard matrix is an orthogonal transform that mixes coordinates by taking sums and differences, and can be viewed as a combination of reflections.
The base matrix is:
\[ H_2=\frac{1}{\sqrt{2}}\begin{bmatrix}1&1\\1&-1\end{bmatrix} \]
And \(4 \times 4\) Hadamard matrix is:
\[ H_4=\frac{1}{\sqrt{2}}\begin{bmatrix}H_2&H_2\\H_2&-H_2\end{bmatrix}=\frac{1}{2}\begin{bmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\end{bmatrix} \]
This construction gives Hadamard matrices of size \(2^m\) (Sylvester type). More generally, Hadamard matrices exist for many orders \(N=4k\), and existence for every \(4k\) is the Hadamard conjecture.
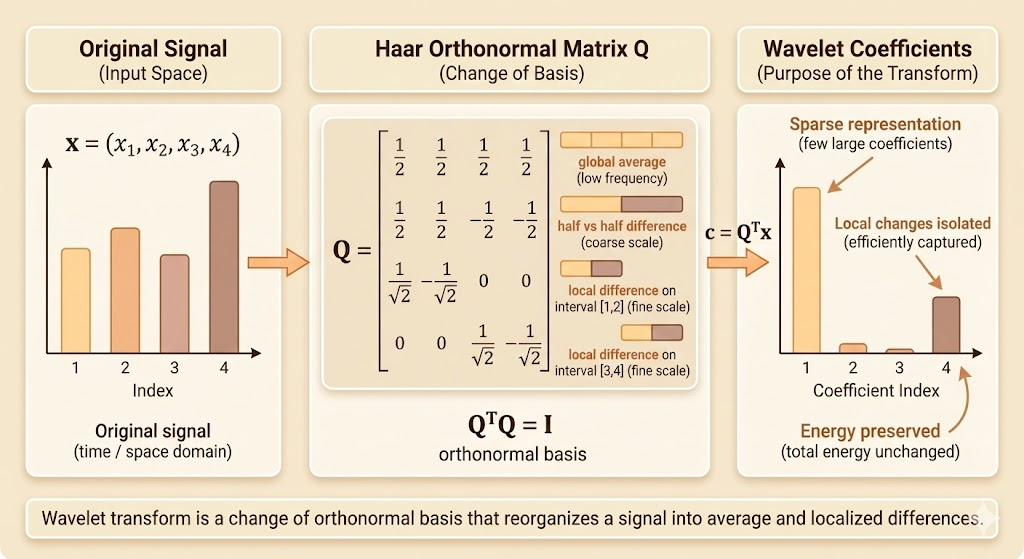
Wavelets
Wavelets form an orthonormal basis that captures local structure and multiscale differences in signals.
Example Haar wavelet matrix (orthonormal):
\[ W=\frac{1}{2}\begin{bmatrix} 1 & 1 & \sqrt{2} & 0 \\ 1 & 1 & -\sqrt{2} & 0 \\ 1 & -1 & 0 & \sqrt{2} \\ 1 & -1 & 0 & -\sqrt{2} \end{bmatrix} \]
Eigenvectors of Symmetric Matrices
The eigenvectors of symmetric matrices and orthogonal matrices are orthogonal.
Eigenvectors of the following permutation matrix (orthogonal):
\[ \begin{bmatrix}0&1&0&0\\0&0&1&0\\0&0&0&1\\1&0&0&0\end{bmatrix} \]
are discrete Fourier transforms:
\[ \frac{1}{2} \begin{bmatrix} 1 & 1 & 1 & 1 \\ -1 & i & -i & 1 \\ 1 & -1 & -1 & 1 \\ -1 & -i & i & 1 \end{bmatrix} \]
Exercise
1. Draw unit vectors \(u\) and \(v\) that are not orthogonal. Show that \(w = v - u(u^\top v)\) is orthogonal to \(u\) (and add \(w\) to your picture).
Solution:
\[ (v-u(u^\top v))^\top u = v^\top u - u^\top u \cdot u^\top v \]
Because \(u\) is a unit vector, \(u^\top u = 1\), thus:
\[ v^\top u - u^\top u \cdot u^\top v = 0 \]
2. Key property of every orthogonal matrix: \(\|Qx\|^2 = \|x\|^2\) for every vector \(x\). More than this, show that \((Qx)^\top(Qy) = x^\top y\) for every vector \(x\) and \(y\). So lengths and angles are not changed by \(Q\).
Solution:
\[ (Qx)^\top(Qy) = x^\top Q^\top Q y = x^\top I y = x^\top y \]
3. A permutation matrix has the same columns as the identity matrix (in some order). Explain why this permutation matrix and every permutation matrix is orthogonal:
\[ P = \begin{bmatrix}0&1&0&0\\0&0&1&0\\0&0&0&1\\1&0&0&0\end{bmatrix} \]
has orthonormal columns so \(P^\top P = I\) and \(P^{-1} = P^\top\).
Solution:
The reason why \(P\) is orthonormal is:
- Each column of \(P\) is one of the standard basis vectors, so \(\|p_j\| = 1\).
- Two different columns are different basis vectors, so \(p_i^\top p_j = 0\) for \(i \neq j\).