MIT 18.065: Lecture 15 - Matrix Derivatives and Eigenvalue Changes
Matrix Derivatives and Eigenvalue Changes
This lecture studies how matrices and their spectral quantities change with time. We derive formulas for the derivative of a matrix inverse, the derivative of an eigenvalue, and the effect of low-rank updates.
Derivative of the matrix inverse
Let \(A(t)\) be invertible for all \(t\). Differentiate the identity \[ A^{-1}(t)A(t)=I \] to get \[ \frac{dA^{-1}}{dt}A + A^{-1}\frac{dA}{dt}=0. \] Multiplying on the right by \(A^{-1}\) gives the standard formula \[ \frac{dA^{-1}}{dt}=-A^{-1}\frac{dA}{dt}A^{-1}. \]
Derivative of an eigenvalue
Suppose \[ A(t)x(t)=\lambda(t)x(t), \] with left eigenvector \(y(t)\) defined by \[ y(t)^\top A(t)=\lambda(t)y(t)^\top. \] Normalize so that \(y^\top x=1\). Then \[ \lambda(t)=y(t)^\top A(t)x(t). \] Differentiating gives \[ \frac{d\lambda}{dt}=\frac{dy^\top}{dt}A x + y^\top\frac{dA}{dt}x + y^\top A\frac{dx}{dt}. \] Using \(Ax=\lambda x\), \(y^\top A=\lambda y^\top\), and the normalization \(\frac{d}{dt}(y^\top x)=0\), the first and third terms cancel. Therefore \[ \frac{d\lambda}{dt}=y^\top\frac{dA}{dt}x. \] For symmetric \(A(t)\), we can take \(y=x\), so \(\dot\lambda = x^\top \dot A\,x\).
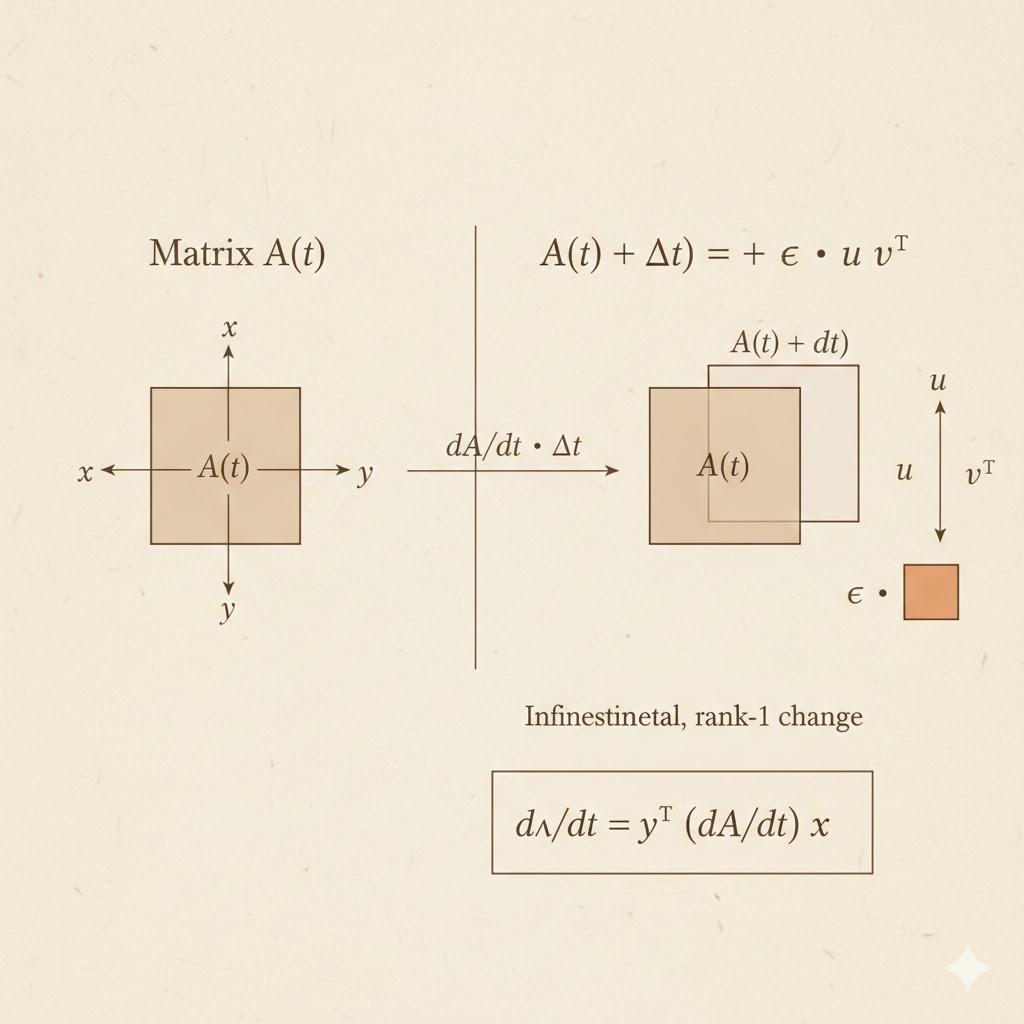
Eigenvalue changes under low-rank updates
Let \(S\in\mathbb{R}^{n\times n}\) be symmetric with eigenvalues \[ \lambda_1\ge \lambda_2\ge \cdots\ge \lambda_n. \] Consider a positive semidefinite update \(S\mapsto S+UU^\top\) of rank \(k\) and denote the updated eigenvalues by \[ \gamma_1\ge \gamma_2\ge \cdots\ge \gamma_n. \]
Rank-1 update (interlacing)
For \(S+uu^\top\) (rank-1, PSD), all eigenvalues increase: \(\gamma_i\ge \lambda_i\). In addition, the spectra interlace: \[ \gamma_1\ge \lambda_1\ge \gamma_2\ge \lambda_2\ge \cdots\ge \gamma_n\ge \lambda_n. \] Equivalently, for \(i\ge 2\), \[ \lambda_i\le \gamma_i\le \lambda_{i-1}. \]
Rank-2 update (wider interlacing)
For \(S+UU^\top\) with \(\mathrm{rank}(U)=2\), eigenvalues can move up by at most two positions in the ordering. For \(i\ge 3\), \[ \lambda_i\le \gamma_i\le \lambda_{i-2}. \] The top two eigenvalues have no comparable upper bound beyond monotonicity.
Rank-\(k\) update (general case)
In general, a rank-\(k\) PSD update yields the interlacing bound \[ \lambda_i\le \gamma_i\le \lambda_{i-k},\quad i\ge k+1, \] with the convention that \(\lambda_j=+\infty\) for \(j\le 0\). This captures the idea that a rank-\(k\) update can shift any eigenvalue upward by at most \(k\) positions.