Lecture 2: Multiplying and Factoring Matrices
Overview
- Five common ways to factor a matrix (\(LU\), \(QR\), spectral, diagonalization, SVD)
- Elimination as a sum of rank-1 updates
- Four fundamental subspaces and a null space example
Five Ways to Factor a Matrix
- \(LU\): elimination with lower and upper triangular matrices
- \(QR\): orthonormal columns times an upper triangular matrix
- Spectral: \(S = Q\Lambda Q^{\top}\) for symmetric matrices
- Diagonalization: \(A = X\Lambda X^{-1}\) for eigenvectors
- SVD: \(A = U\Sigma V^{\top}\) for any matrix
LU Factorization
Elimination factors a matrix into a lower and upper triangular pair.
Example (2x2)
\[ A=\begin{bmatrix}2&3\\4&7\end{bmatrix} \]
Eliminate row 2 by \(\text{row}_2 - 2(\text{row}_1)\):
\[ U=\begin{bmatrix}2&3\\0&1\end{bmatrix} \]
The first row of \(L\) is \(\begin{bmatrix}1&0\end{bmatrix}\), and the second row is \(\begin{bmatrix}2&1\end{bmatrix}\) because \[ \text{row}_{A2} = 2(\text{row}_{U1}) + 1(\text{row}_{U2}) \]
So \[ L=\begin{bmatrix}1&0\\2&1\end{bmatrix},\quad A=LU \]
Elimination as Rank-1 Updates
Elimination can be viewed as a sum of rank-1 matrices:
\[ A \rightarrow (\text{Col}_1\text{Row}_1) + \begin{bmatrix}0&\dots&0\\0&A_2\end{bmatrix} \]
Using the same example:
\[ \begin{bmatrix}2&3\\4&7\end{bmatrix} \rightarrow \begin{bmatrix}2&3\\4&6\end{bmatrix}_{\text{rank }1} \;+\; \begin{bmatrix}0&0\\0&1\end{bmatrix}_{\text{rank }1} \]
So \[ LU=(l_1u_1^{\top})_{\text{rank }1} + (l_2u_2^{\top})_{\text{rank }1} \]

Spectral Decomposition
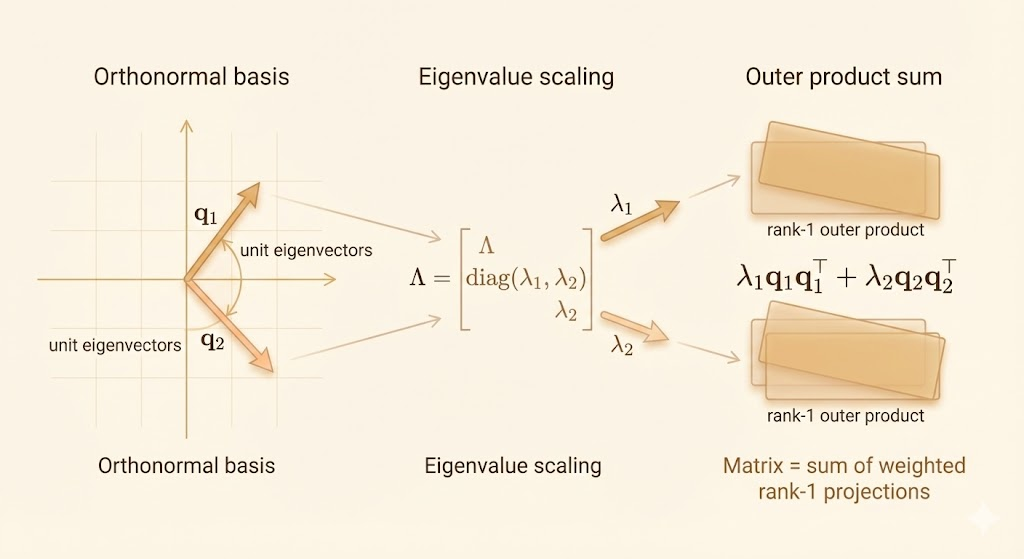
We can rewrite \[ S=(Q\Lambda)Q^{\top}=\sum_k \text{Col}_k(Q\Lambda)\,\text{Row}_k(Q^{\top}) \]
Each \(\text{Col}_k(Q\Lambda)\text{Row}_k(Q^{\top})\) is rank-1.
Columns of Q scaled by Lambda
\[ \begin{bmatrix}|&\dots&|\\ q_1&\dots&q_n\\ |&\dots&|\end{bmatrix} \begin{bmatrix}\lambda_1&\dots&0\\ \dots&\dots&\dots\\ 0&\dots&\lambda_n\end{bmatrix} \]
So the columns are \(q_1\lambda_1,\dots,q_n\lambda_n\).
This gives: \[ S = \sum_{i=1}^n \lambda_i q_i q_i^{\top} \]
Check
Multiply by \(q_1\): \[ Sq_1 = \sum_{i=1}^n \lambda_i q_i q_i^{\top} q_1 \]
Because \(q_i^{\top}q_1=0\) for \(i\ne 1\) and \(q_1^{\top}q_1=1\): \[ Sq_1=\lambda_1 q_1 \]
Diagonalization: \(A = X\Lambda X^{-1}\)
Eigenvectors in \(X\) and eigenvalues in \(\Lambda\) give a diagonal form of \(A\).
Singular Value Decomposition: \(A = U\Sigma V^{\top}\)
- \(U\): orthogonal
- \(\Sigma\): diagonal (singular values)
- \(V\): orthogonal
Four Fundamental Subspaces
For an \(m \times n\) matrix \(A\) with rank \(r\):
- Column space \(C(A)\): subspace of \(\mathbb{R}^m\), dimension \(r\)
- Row space \(C(A^{\top})\): subspace of \(\mathbb{R}^n\), dimension \(r\)
- Null space \(N(A)\): subspace of \(\mathbb{R}^n\), dimension \(n-r\)
- Left null space \(N(A^{\top})\): subspace of \(\mathbb{R}^m\), dimension \(m-r\)
Null Space
Null space is all solutions to \(Ax=0\).
Properties: - If \(Ax=0\) and \(Ay=0\), then \(A(x+y)=0\) - If \(Ax=0\), then \(A(cx)=0\)
These show the null space is a subspace.
Example
\[ A=\begin{bmatrix}1&2&4\\2&4&8\end{bmatrix} \]
- \(m=2\), \(n=3\), rank \(r=1\)
- Null space dimension: \(n-r=2\)
- Two independent null space vectors: \(\begin{bmatrix}-4\\0\\1\end{bmatrix}\), \(\begin{bmatrix}0\\-2\\1\end{bmatrix}\)
Rows of \(A\) are orthogonal to vectors in the null space.
Exercises
Suppose \(a\) and \(b\) are column vectors with components \(a_1,\dots,a_m\) and \(b_1,\dots,b_p\).
Can you multiply \(ab^{\top}\)? What is the shape? What is entry \((i,j)\)? What can you say about \(aa^{\top}\)?We can multiply \(ab^{\top}\); the shape is \(m\times p\).
Entry \((i,j)\) equals \(a_i b_j\).\(aa^{\top}\):
- square (\(m\times m\))
- symmetric: \((aa^{\top})^{\top}=aa^{\top}\)
- rank 1
- PSD: \(x^{\top}aa^{\top}x=(a^{\top}x)^2\ge 0\)

Exercise 1 solution If \(A\) has columns \(a_1,a_2,a_3\) and \(B=I\), what are the rank-1 matrices \(a_1b_1^{\top}\), \(a_2b_2^{\top}\), \(a_3b_3^{\top}\)? They should add to \(AI=A\).
- \(a_1b_1^{\top}\):
\[ a_1b_1^{\top} = \begin{bmatrix}|&|&|\\ a_1&0&0\\ |&|&|\end{bmatrix} \]
- \(a_2b_2^{\top}\):
\[ a_2b_2^{\top} = \begin{bmatrix}|&|&|\\ 0&a_2&0\\ |&|&|\end{bmatrix} \]
- \(a_3b_3^{\top}\):
\[ a_3b_3^{\top} = \begin{bmatrix}|&|&|\\ 0&0&a_3\\ |&|&|\end{bmatrix} \]