Lecture 5: Positive Definite and Semidefinite Matrices
Positive Definite Properties
- All \(\lambda_i > 0\)
- Energy: \(x^\top Sx> 0 \quad \forall x\ne 0\)
- \(S=AA^\top\) (A is full rank)
- All leading determinants >0
- All pivots in elimination >0
Equivalent tests (for symmetric \(S\)): - All eigenvalues are positive - Cholesky exists with positive pivots (same as positive leading principal minors)
Positive Semidefinite Properties
- \(\lambda_i \ge 0\)
- \(x^\top Sx \ge 0\)
- \(S= AA^\top\) (A may be rectangular; not full rank)
- Leading determinants \(\ge 0\)
- r pivots \(> 0\), \(r \le n\)

Graph of Positive Definite Matrices
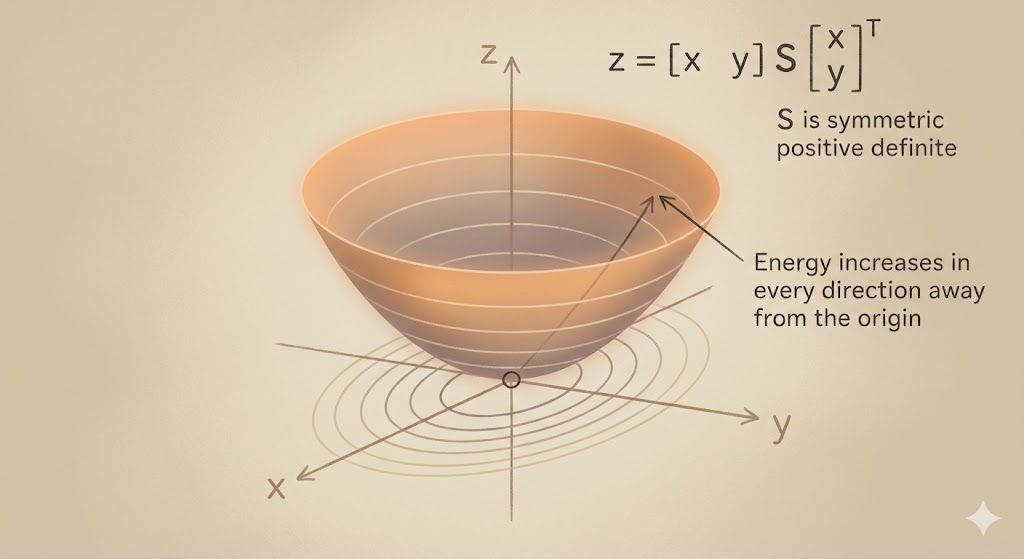
For a positive definite matrix, the quadratic form \(x^\top S x\) is an energy bowl: minimum at the origin, rising in every direction.
Deep learning formulates learning as minimizing a scalar objective (loss), analogous to minimizing an energy landscape.
Convexity
The graph is convex.
Gradient Descent
To find the minimal point, we can use gradient descent:
- Start from point \([x_0,y_0]\)
- Calculate the gradient (first derivative of parameters) \(\nabla f\) of the function at \([x_0,y_0]\)
- Take a small step in the direction of the negative gradient
- Repeat the process until convergence
Exercises
1. If S and T are both positive definite, is S+T positive definite?
Solution: Yes. From energy form: \(x^\top(S+T)x=x^\top Sx+x^\top T x >0\)
2. If S is positive definite, is \(S^{-1}\) positive definite?
Solution: Yes. Eigenvalues of \(S^{-1}\) equals to \(\frac{1}{\lambda}\), where \(\lambda\) are eigenvalues of S.
3. Is \(Q^{-1}SQ\) positive definite if Q is orthogonal and S is symmetric positive definite?
Solution: Yes. 1. It is similar to S so the eigenvalues are the same 2. From energy form, \(x^\top Q^\top S Qx=(Qx)^\top S (Qx)\)
4. For which numbers b and c are these matrices positive definite?
\[ S_1=\begin{bmatrix}1&b\\b&9\end{bmatrix},\quad S_2=\begin{bmatrix}2&4\\4&c\end{bmatrix},\quad S_3=\begin{bmatrix}c&b\\b&c\end{bmatrix} \]
Solution:
- \(S_1\): \(|b| <3\)
- \(S_2\): \(c > 8\)
- \(S_3\): \(c > |b|\)
With the pivots in D and multiplier in L, factor each A into \(LDL^\top\):
\[ S_1=\begin{bmatrix}1&0\\b&1\end{bmatrix}\begin{bmatrix}1&0\\0&9-b^2\end{bmatrix}\begin{bmatrix}1&b\\0&1\end{bmatrix} \]
\[ S_2=\begin{bmatrix}1&0\\2&1\end{bmatrix}\begin{bmatrix}2&0\\0&c-8\end{bmatrix}\begin{bmatrix}1&2\\0&1\end{bmatrix} \]
\[ S_3=\begin{bmatrix}1&0\\\frac{b}{c}&1\end{bmatrix}\begin{bmatrix}c&0\\0&c-\frac{b^2}{c}\end{bmatrix}\begin{bmatrix}1&\frac{b}{c}\\0&1\end{bmatrix} \]
5. Find the 3 by 3 matrix S and its pivots, rank, eigenvalues, and determinant:
\[ \begin{bmatrix}x_1&x_2&x_3\end{bmatrix}\begin{bmatrix}S\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=4(x_1-x_2+2x_3)^2 \]
Solution:
Set \(a=\begin{bmatrix}1\\-1\\2\end{bmatrix}\), then \(4(x_1-x_2+2x_3)^2=4(a^\top x)^2=x^\top (4 a a^\top) x\)
\[ S= 4a a^\top=\begin{bmatrix}4&-4&8\\-4&4&-8\\8&-8&16\end{bmatrix} \]
- Rank of S is 1
- Determinant is 0
- Eigenvalues: 24, 0, 0
- Pivots: 4, 0, 0
6. Compute the three upper left determinants of S to establish positive definiteness. Verify that their ratios give the second and third pivots.
\[ S=\begin{bmatrix}2&2&0\\2&5&3\\0&3&8\end{bmatrix} \]
Solution:
- Leading determinants: 2, 6, 30
- Pivots: 2, 6/2=3, 30/6=5
Check:
- Row 1: \(2x_1+2x_2\)
- Eliminate \(x_1\):
- row2 - 1×row1: \(3x_2+3x_3\)
- row3 (because \(x_1\) ratio in row3 is already 0)
- row3 - \(\text{row2}_{\text{new}}\): \(5x_3\)