EE 364A (Convex Optimization): Chapter 5.1 - The Lagrange Dual Function
The Lagrange dual function
The Lagrangian turns constrained optimization into an unconstrained objective by penalizing violations with multipliers. The dual function then takes the best (lowest) Lagrangian value over \(x\), yielding a concave function that provides global lower bounds on the primal optimal value.
Lagrangian (standard form)
Consider the standard form problem \[ \begin{aligned} \text{minimize} &\quad f_0(x) \\ \text{subject to} &\quad f_i(x) \le 0,\quad i=1,\dots,m \\ &\quad h_i(x)=0,\quad i=1,\dots,p, \end{aligned} \] with \(x\in\mathbb{R}^n\) and domain \(\mathcal{D}\).
The Lagrangian is \[ L(x,\lambda,\nu)=f_0(x)+\sum_{i=1}^m \lambda_i f_i(x)+\sum_{i=1}^p \nu_i h_i(x), \] with multipliers \(\lambda\in\mathbb{R}^m\) and \(\nu\in\mathbb{R}^p\).
- \(L: \mathbb{R}^n\times\mathbb{R}^m\times\mathbb{R}^p\to\mathbb{R}\)
- \(\mathrm{dom}\,L=\mathcal{D}\times\mathbb{R}^m\times\mathbb{R}^p\)
- Each \(\lambda_i\ge 0\) penalizes inequality violations \(f_i(x)\le 0\)
- Each \(\nu_i\) enforces equality constraints \(h_i(x)=0\)
Lagrange dual function
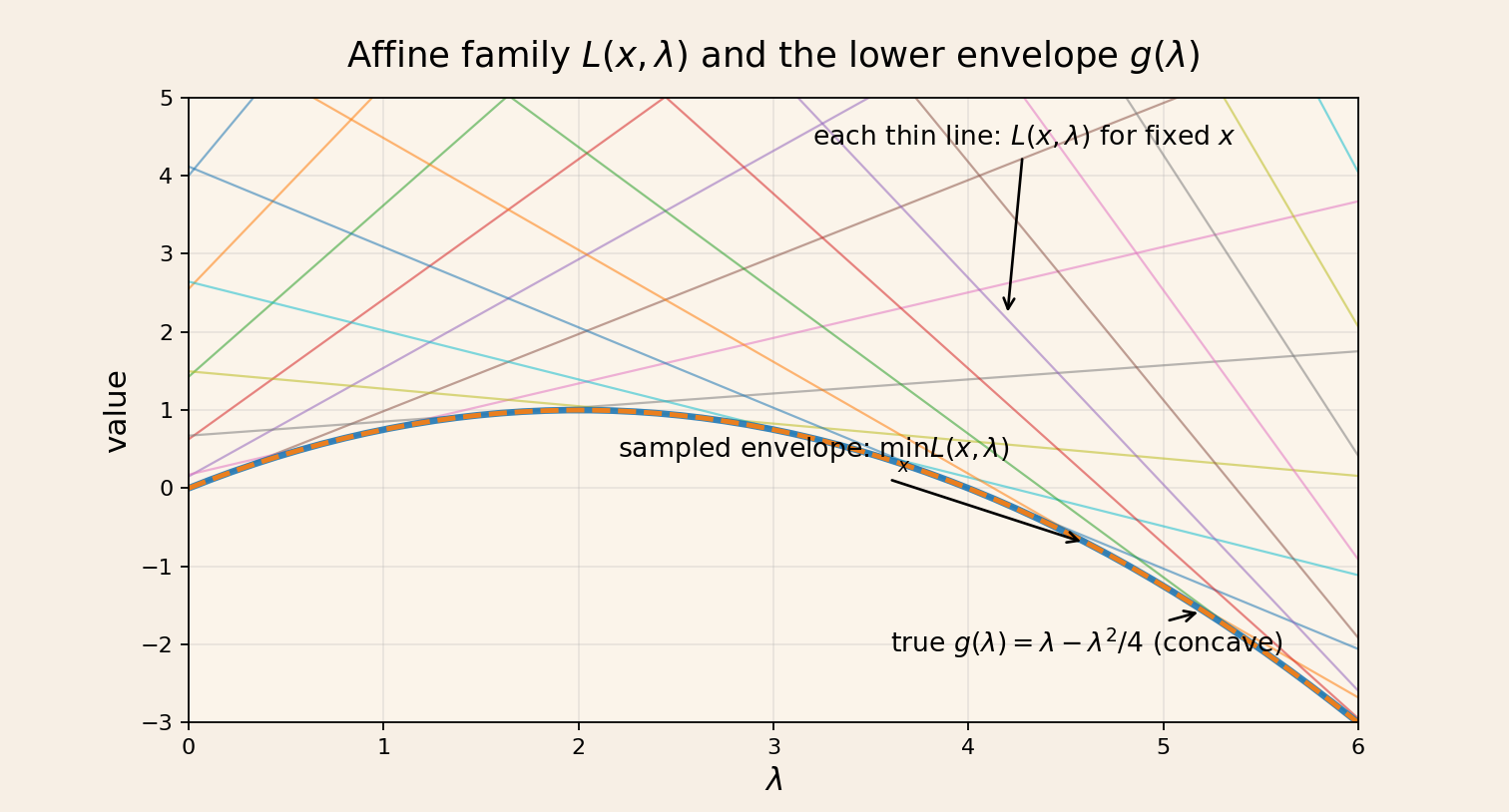
The dual function is the pointwise infimum of the Lagrangian over \(x\): \[ g(\lambda,\nu)=\inf_{x\in\mathcal{D}} L(x,\lambda,\nu). \] Key facts: - \(g\) is a pointwise infimum of affine functions in \((\lambda,\nu)\) - Therefore, \(g\) is concave even if the primal problem is not convex
Lower bounds on the optimal value
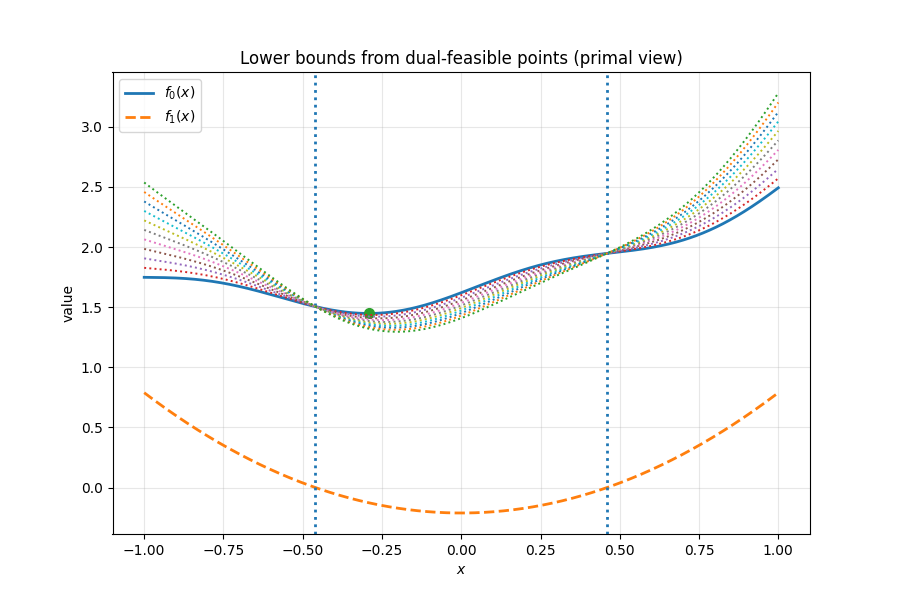
Let \(p^*\) be the primal optimal value. For any feasible \(\tilde{x}\) and any \(\lambda\succeq 0\), \[ \sum_{i=1}^m \lambda_i f_i(\tilde{x})\le 0,\qquad h_i(\tilde{x})=0. \] So \[ L(\tilde{x},\lambda,\nu) =f_0(\tilde{x})+\sum_{i=1}^m \lambda_i f_i(\tilde{x})+\sum_{i=1}^p \nu_i h_i(\tilde{x}) \le f_0(\tilde{x}). \] Taking the infimum over \(x\) yields \[ g(\lambda,\nu)\le f_0(\tilde{x})\quad \text{for every feasible }\tilde{x}. \] Therefore, \[ \boxed{g(\lambda,\nu)\le p^*} \] for all \(\lambda\succeq 0\). The dual function gives a global lower bound on the primal optimum. The bound is only nontrivial when \(g(\lambda,\nu)>-\infty\).
Linear approximation interpretation
The Lagrangian does not enforce feasibility. Instead, it replaces constraints by linear penalties. For each \(\lambda\ge 0\), the function \(L(x,\lambda)\) lies below \(f_0(x)\) on the feasible set, so its minimum gives a lower bound on \(p^*\). Maximizing \(g(\lambda)\) over \(\lambda\ge 0\) finds the tightest such lower bound.
Examples
Least-norm solution to \(Ax=b\) (underdetermined)
\[ \begin{aligned} \text{minimize} &\quad x^\top x \\ \text{subject to} &\quad Ax=b \end{aligned} \]
The Lagrangian is \[ L(x,\nu)=x^\top x+\nu^\top(Ax-b). \] Stationarity gives \[ \nabla_x L=2x+A^\top \nu=0\quad\Rightarrow\quad x=-\tfrac{1}{2}A^\top\nu. \] Substituting back, \[ g(\nu)=\inf_x L(x,\nu)= -\tfrac{1}{4}\,\nu^\top A A^\top\nu - b^\top\nu. \] The dual is a concave quadratic maximization in \(\nu\).
Standard linear program
\[ \begin{aligned} \text{minimize} &\quad c^\top x \\ \text{subject to} &\quad Ax=b \\ &\quad x\succeq 0. \end{aligned} \] Rewrite \(x\succeq 0\) as \(-x_i\le 0\) with multipliers \(\lambda\succeq 0\): \[ L(x,\lambda,\nu)=c^\top x-\lambda^\top x+\nu^\top(Ax-b)=-b^\top\nu+(c+A^\top\nu-\lambda)^\top x. \] The infimum over \(x\) is finite only if \(c+A^\top\nu-\lambda=0\) with \(\lambda\succeq 0\). Thus \[ g(\lambda,\nu)=\begin{cases} -b^\top \nu, & c+A^\top\nu-\lambda=0,\ \lambda\succeq 0, \\ -\infty, & \text{otherwise}. \end{cases} \] Eliminating \(\lambda\) gives the dual constraint \(A^\top\nu + c\succeq 0\).
Conjugate function connection
The conjugate of a function \(f:\mathbb{R}^n\to\mathbb{R}\cup\{+\infty\}\) is \[ f^*(y)=\sup_{x\in\mathrm{dom}\,f}\,(y^\top x-f(x)). \] Consider the equality-constrained problem \[ \begin{aligned} \text{minimize} &\quad f(x) \\ \text{subject to} &\quad x=0. \end{aligned} \] Its Lagrangian is \(L(x,\nu)=f(x)+\nu^\top x\), so the dual function is \[ \begin{aligned} g(\nu) &=\inf_x\big(f(x)+\nu^\top x\big) \\ &=-\sup_x\big(-f(x)-\nu^\top x\big) \\ &=-f^*(-\nu). \end{aligned} \] So the dual function is the negative conjugate of \(f\) evaluated at \(-\nu\).
More generally, for \[ \text{minimize } f(x)\quad\text{subject to } Ax=b, \] we have \[ g(\nu)=\inf_x\big(f(x)+\nu^\top(Ax-b)\big)=-f^*(-A^\top\nu)-b^\top\nu. \] This explains why conjugate functions appear throughout duality: taking the infimum of the Lagrangian in \(x\) is exactly a conjugate transform.