EE 364A (Convex Optimization): Chapter 4.2 - Convex Optimization
Convex Optimization Textbook - Chapter 4.2 (page 150)
Convex Problems in Standard Form
A convex optimization problem in standard form is
\[ \begin{aligned} \text{minimize} \quad & f_0(x) \\ \text{subject to} \quad & f_i(x) \le 0, \quad i = 1,\dots,m \\ & a_i^\top x = b_i, \quad i = 1,\dots,p, \end{aligned} \]
where \(f_0,\dots,f_m\) are convex and the equality constraints are affine. The feasible set is
\[ \mathcal{D} = \bigcap_{i=0}^m \mathrm{dom}\, f_i, \]
which is convex because it is an intersection of convex sets. Affine equalities preserve convexity, so the feasible region remains convex.
If \(h(x) = 0\) is part of the feasible set, we need \(h(\theta x + (1-\theta)y) = 0\) whenever \(h(x)=h(y)=0\). This holds exactly when \(h\) is affine: \(h(\theta x + (1-\theta)y) = \theta h(x) + (1-\theta)h(y)\).
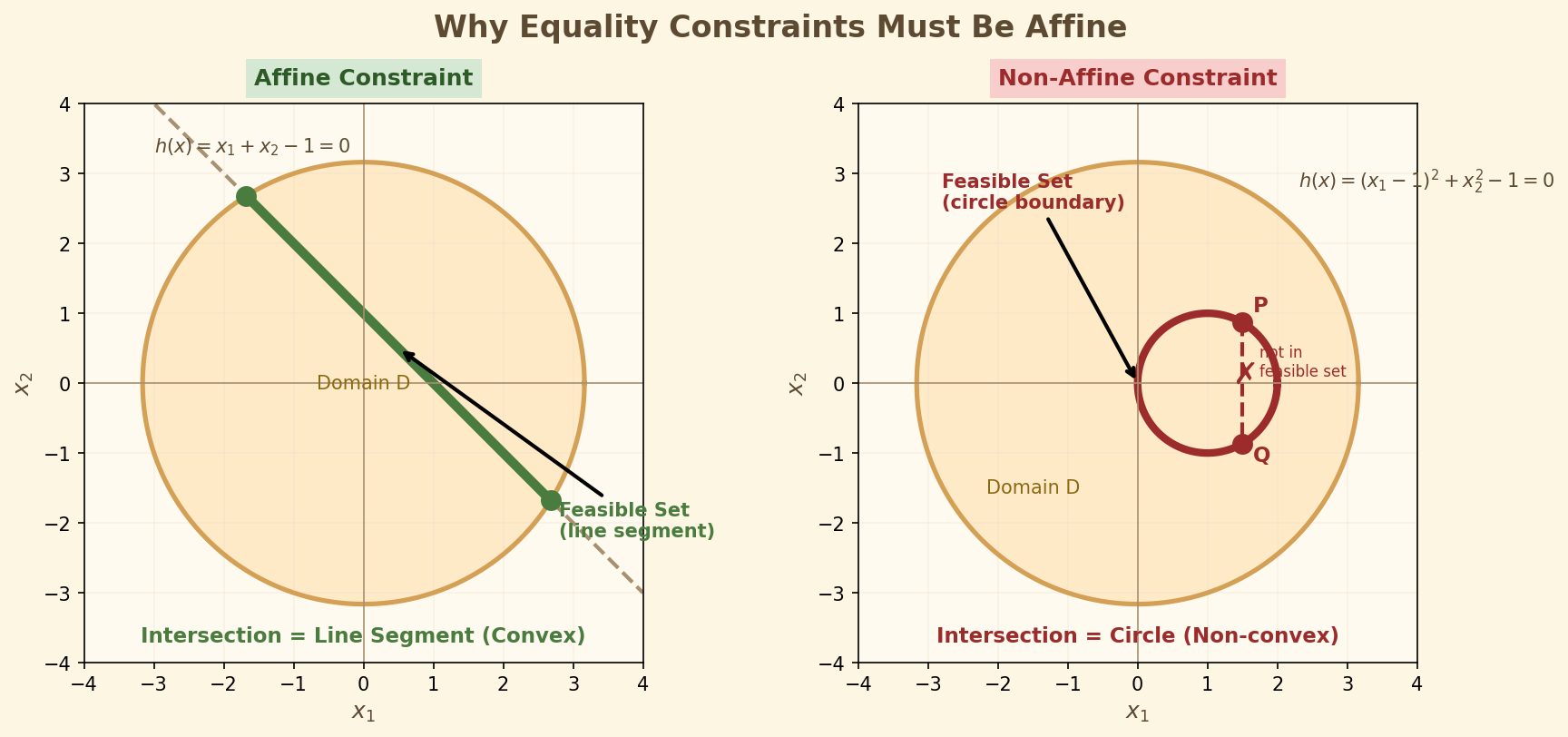
Local vs Global Optimality
For convex problems, every local optimum is a global optimum. Sketch:
- Assume \(x\) is locally optimal inside a ball of radius \(R\), so \(f_0(x) \le f_0(z)\) for all feasible \(z\) with \(\|z-x\|_2 < R\).
- Suppose there exists a feasible \(y\) with \(f_0(y) < f_0(x)\) (a better point outside the ball).
- By convexity, points on the segment \(z = (1-\theta)x + \theta y\) satisfy \(f_0(z) < (1-\theta)f_0(x) + \theta f_0(y) < f_0(x)\) for \(0 < \theta \le 1\).
- For small \(\theta\), \(z\) stays inside the ball, contradicting local optimality.
Geometric takeaway: convexity rules out spurious local minima.
First-Order Optimality (Differentiable \(f_0\))
For differentiable \(f_0\) and any \(x,y \in \mathrm{dom}\, f_0\),
\[ f_0(y) \ge f_0(x) + \nabla f_0(x)^\top (y-x). \]
A feasible point \(x^\star\) is optimal iff
\[ \nabla f_0(x^\star)^\top (y - x^\star) \ge 0 \quad \forall y \text{ feasible}. \]
- Unconstrained: \(\nabla f_0(x^\star) = 0\).
- Equality constraints \(Ax=b\): \(\nabla f_0(x^\star)\) is orthogonal to the nullspace of \(A\), so \(\nabla f_0(x^\star) + A^\top v = 0\) for some \(v\).
- Nonnegative orthant (\(x \succeq 0\)): \(x \succeq 0\), \(\nabla f_0(x) \succeq 0\), and \(x_i (\nabla f_0(x))_i = 0\) (complementary slackness).
Equivalent Convex Problems
Two convex problems are equivalent if solving one immediately yields a solution to the other.
- Change of variables: \(x = Fz + x_0\) with \(F\) spanning the nullspace of equality constraints removes those equalities.
- Transforming objective/constraints: Apply a monotone increasing function to \(f_0\) or \(f_i\) without changing the solution (e.g., minimize \(\|Ax-b\|_2\) vs. \(\|Ax-b\|_2^2\)).
- Slack variables: Replace \(a^\top x \le b\) by \(a^\top x + s = b\), \(s \ge 0\) to expose feasibility structure.
- Epigraph form: Introducing \(t\) so that \(f_0(x) \le t\) converts nonlinear objectives to constraints when useful for decomposition.
Quasiconvex Problems and Bisection
A quasiconvex problem in standard form:
- Minimize \(f_0(x)\) where \(f_0\) is quasiconvex
- Subject to \(f_i(x) \le 0\) (convex) and \(Ax = b\)
Quasiconvexity is characterized by convex sublevel sets. If a family of convex inequalities \(\phi_t(x) \le 0\) satisfies \(f_0(x) \le t \Leftrightarrow \phi_t(x) \le 0\), feasibility at level \(t\) reveals whether \(p^\star \le t\).
Bisection on the Optimal Value
Pick bounds \(l \le p^\star \le u\) and tolerance \(\epsilon > 0\):
- Set \(t = (l+u)/2\).
- Solve the feasibility problem: find \(x\) s.t. \(\phi_t(x) \le 0\), \(f_i(x) \le 0\), \(Ax=b\).
- If feasible, \(u \gets t\); else, \(l \gets t\).
- Repeat until \(u - l < \epsilon\).
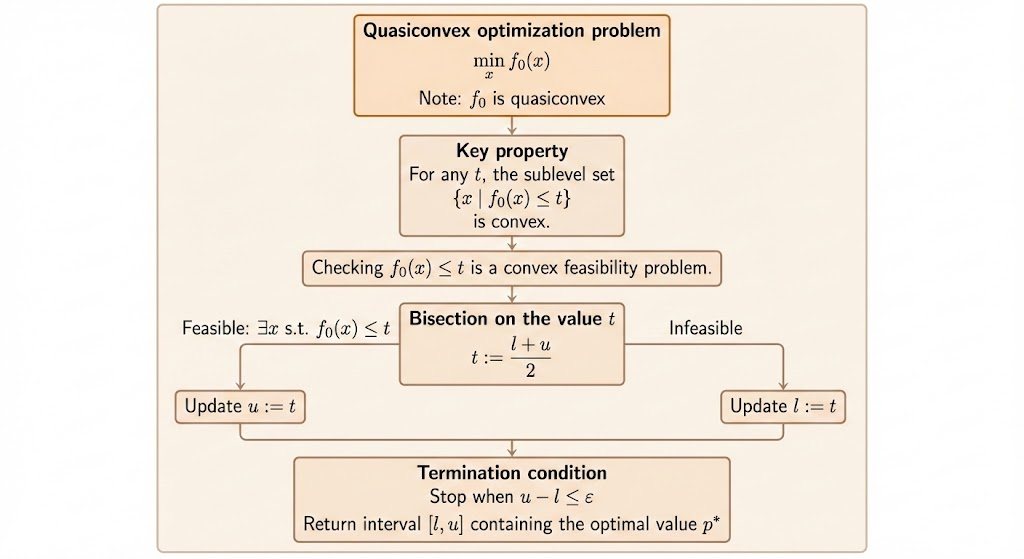
The method converts a quasiconvex minimization into a sequence of convex feasibility checks.
Takeaways
- Convexity of objective and constraints ensures the feasible set is convex and local minima are global.
- First-order conditions simplify to projected gradient orthogonality plus complementary slackness for inequality constraints.
- Problem equivalence (change of variables, slack variables, epigraphs) is a practical toolkit for simplifying formulations.
- Quasiconvex problems retain tractability via bisection on sublevel-set feasibility.