Gilbert Strang’s Calculus: The Exponential Function
Properties
- \(\frac{d}{dx}e^x = e^x\)
- \(e^a\cdot e^b = e^{a+b}\)
- If \(y=e^{cx}\), then \(\frac{dy}{dx}=cy=c e^{cx}\)
Infer the value of \(e\)
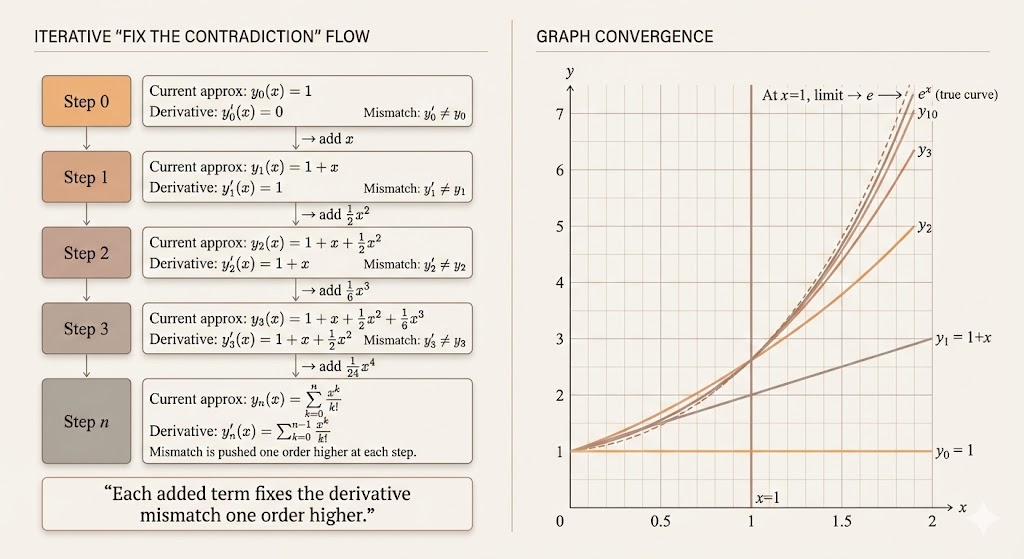
Start from the condition that defines the exponential function:
- \(y(0)=1\)
- \(\frac{dy}{dx}=y\)
If we start with \(y(x)=1\), then
- \(y(x)=1\)
- \(y'(x)=0\)
This cannot satisfy \(y'=y\), so we need to add an \(x\) term.
Step 1:
- \(y(x)=1+x\)
- \(y'(x)=1\)
Now \(y'\) is still missing the \(x\) term, so we add a quadratic term.
Step 2:
- \(y(x)=1+x+\frac{1}{2}x^2\)
- \(y'(x)=1+x\)
Now \(y'\) is missing \(\frac12 x^2\), so we add a cubic term.
Step 3:
- \(y(x)=1+x+\frac{1}{2}x^2+\frac{1}{6}x^3\)
- \(y'(x)=1+x+\frac{1}{2}x^2\)
Key observation:
- This is an infinite correction loop.
- Each time we add a term \(\frac{1}{n!}x^n\), its derivative becomes \(\frac{1}{(n-1)!}x^{n-1}\), exactly matching the previous missing term.
So eventually, \[ y(x)=1+x+\frac{1}{2}x^2+\frac{1}{6}x^3+\cdots+\frac{1}{n!}x^n+\cdots \]
When \(x=1\), we get \[ e=1+1+\frac{1}{2}+\frac{1}{6}+\frac{1}{24}+\cdots+\frac{1}{n!}+\cdots \approx 2.718281828459045. \]
We are not guessing \(e^x\). We are forcing a function to equal its own derivative, and factorial coefficients are exactly what make this possible.
Graph of \(e^x\)
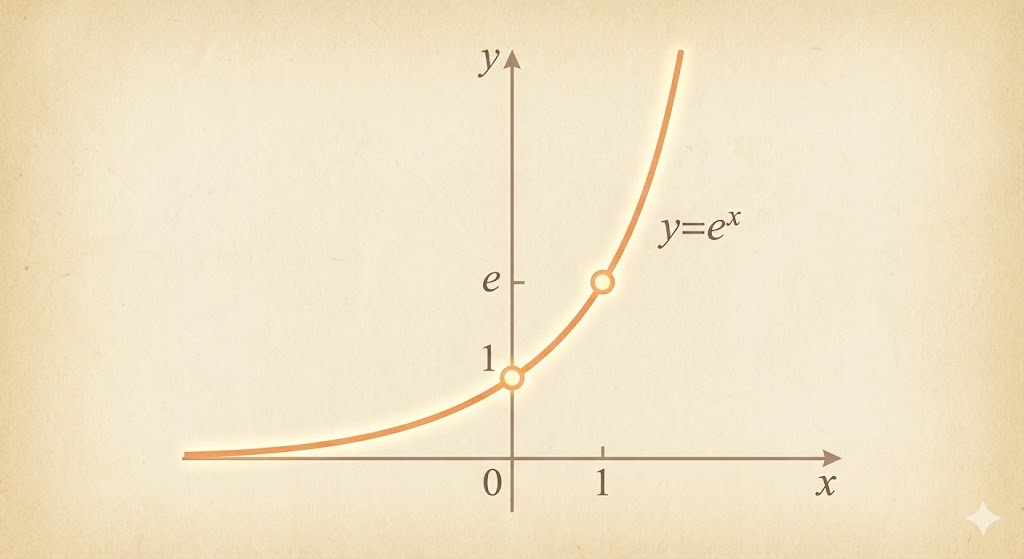
- At \(x=0\), \(y=1\).
- At \(x=1\), \(y=e\).
- For \(x<0\), \(0<e^x<1\).
- \(e^{-x}=\frac{1}{e^x}\).
- The slope is always positive and increases with \(x\).
Example: Computing Compound Interest
Suppose you have $$1 in the bank, with 100% annual interest.
If interest is compounded yearly:
- End of year 1: \(\$2\)
- End of year 2: \(\$4\)
- End of year 3: \(\$8\)
So after \(n\) years, the amount is \(2^n\).
If the same annual rate is compounded monthly, then after one year: \[ \left(1+\frac{1}{12}\right)^{12} \approx 2.613035290224676. \]
If it is compounded daily: \[ \left(1+\frac{1}{365}\right)^{365} \approx 2.7145674820219727. \]
As compounding becomes more frequent, the value approaches \(e\): \[ \left(1+\frac{1}{N}\right)^N \to e. \]
That is why \(e\) naturally appears in continuous growth.